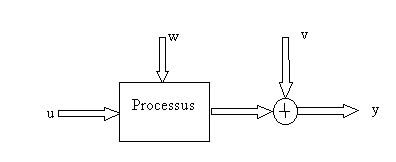
On considère un processus décrit par une représentation díétat discrète, il síagit soit díun processus discret, soit díun processus continu discrétisé.
Exemple : Le SCAO ( système de contrôle et díattitude et díorbite díun satellite ). Le contrôle díattitude est important pour que les caméras du satellite restent pointées sur la terre. Or le satellite a tendance à se dépointer sous líaction de perturbations aléatoires ; celles-ci affectent les états ( attitude et vitesses autour du centre de gravité ) du satellite.
Les capteurs ( gyromètres, senseurs STD et SSD ) pour la mesure des vitesses ( roulis, tangage, lacet ) et d'attitude ainsi que leur chaîne de traitement sont sujets aux bruits (thermique, grenaille, 1 / f, quantifiquation, dérives etc.). N'hésiter pas à consulter l'excellent site du CNES dédié à SPOT4
![]() Problème résolu par le filtre de Kalman
Problème résolu par le filtre de Kalman
Líestimation optimale des états X(i) díun système dynamique soumis à des entrées déterministes et aléatoires à partir de mesures bruitées Y(l), Y(l-1) , Y(-
• ) passées et présentes. Líestimation est optimale au sens díun critère quadratique. Les estimations sont linéaires vis à vis des mesures.Trois types de problème sont envisageables :
i > l : Prédiction : Présente un intérêt lorsque le système devient non mesurable.
i = l : Filtrage : Elimination des bruits de mesure.
i < l : Lissage : Peut être utile pour analyser " après-coup " le comportement díun processus.
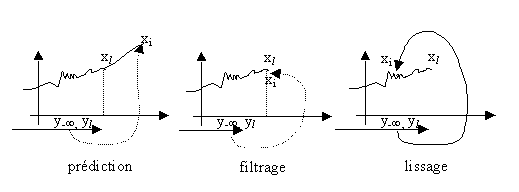
Dans ce cours on envisage le problème du filtrage.
Exemple díapplication du filtre de Kalman au SCAO

Il síagit díestimer au mieux les états ( vitesse et attitude ) du satellite, ce rôle est dévolu au filtre de Kalman. Le but étant ensuite díélaborer une commande optimale qui minimise les écarts de position par rapport à líaxe de pointage terre.
Remarque : Díaprès le théorème de séparation des états, on sépare le problème de líobservation de celui de la commande.
Ā
Observation stochastique des états ( filtre de Kalman ).ā
Elaboration díune loi de commande ( modale, LQ ).Autres exemples díapplication du filtre de Kalman
Guidage du lanceur Ariane ( début des années 80 ).
Application industrielle : La commande des moteurs asynchrones ( 90 % des moteurs utilisés dans líindustrie ) requiert la mesure des flux, de la vitesse et de la position de la machine, ces états sont reconstruits à partir de la mesure des courants statoriques. Au niveau expérimental, líimplantation de filtres de Kalman dédiés à cette application date du milieu des années 90.
Le système évolue dans un environnement bruité et les mesures auxquelles on procède le sont également. Au travers díun exemple, on envisage plusieurs cas de figure pour lesquels le filtre doit fournir la meilleure estimée des états.
Exemple : Suivi de la trajectoire díun lanceur.

1į cas
Le modèle du lanceur est parfaitement connu, il níy a pas de perturbation, les conditions initiales sont connues.
Le modèle a pour équation : ![]() , díaprès les c.i, on résout ð
, díaprès les c.i, on résout ð ![]() .
.
La trajectoire est également obtenue díaprès le modèle ![]()
Dans ce cas, le filtre établit líestimation des états uniquement díaprès le modèle de la représentation díétat. Il vaut mieux ne pas prendre en compte les mesures. Celles-ci, bruitées, entacheraient díerreurs la trajectoire observée.
2į cas
Le modèle est mal identifié, il y a des perturbations, conditions initiales connues.
Le filtre doit générer une estimation optimale des états et des mesures en exploitant au mieux les informations dont il dispose i.e.
- le modèle, les conditions initiales et les commandes ð approche déterministe
- les mesures. Par comparaison des mesures effectuées sur le système à celles que lui fournit líapproche déterministe.
ð
Le filtre fournit|
|
Dans le cas général, líestimation résulte díune pondération entre la connaissance apportée par le modèle et les mesures.
Avant díentrer dans les détails du filtre de Kalman, on rappelle quelques notions de probabilités utiles.
Remarque : Dans les expressions qui suivent les sommations sont continues, cela signifie que les convertisseurs numérique-analogique et analogique-numérique ont un pas de quantifiquation infiniment petit.
p(x1,x2...xn) qui vérifie : Prob(x'< x < xí +dx) = p(x).dx1.dx2...dxn
et ![]() líévénement certain.
líévénement certain.
Illustration dans le cas d'un vecteur à 2 composantes dont les densités de probabilités sont gaussiennes.

![]() La valeur moyenne ou espérance mathématique
La valeur moyenne ou espérance mathématique

Le vecteur est dit centré lorsque E[ X ] = 0
S
xx = Var[X] =S
xx =S
xx=
Ā
La matrice de variance est symétrique définie positive.ā
Les termes diagonaux sont les variances des variables aléatoires : sii2 =É
La trace de la matrice de variance représente la somme des variancesTrace S = ![]()
Ą
Lorsque les composantes non diagonales
Ö
Lorsque la matrice est diagonale, tous les états sont non corrélés.S
xy = Var[X, Y] =La covariance peut porter sur deux vecteurs différents X et Y ou sur un même vecteur considéré à des instants différents [ X(i), X(i + k )].

Figure 6
Sbb(f) représente la distribution fréquentielle de la puissance totale du signal. La densité spectrale de puissance est par définition la transformée de Fourier de la covariance notée Cov[b(i,j)]. Ceci sous réserve que le bruit soit centré et en faisant líhypothèse díergodicité.
On a :
Cov[ b(i,j) ] = F-1{Sbb(f)}
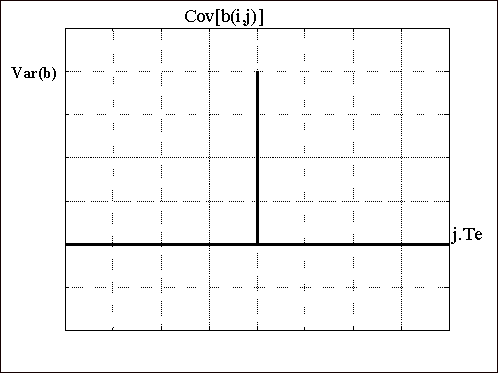
Figure 7
Quelle signification donner à la covariance de b ?
La covariance de b, Cov[b(i,j)] montre comment la valeur prise par b(i.Te) influence la valeur prise par b(i.Te + j.Te ).
Pour j = 0, la ressemblance de b(i.Te) et b(i.Te+ j.Te ) est totale et la covariance Cov[b(i,i)] est égale à Var[b] qui est aussi la puissance du bruit.
Lorsque Cov[b(i,j)] = 0, la valeur prise par b(i.Te) níinfluence pas b( i.Te+ j.Te ). Les bruits sont décorrélés.
La covariance d'un bruit blanc discret s'écrit : ![]()
Avec dij = 0 si i Ļ j et dij = 1 si i = j
On considère le cas díun vecteur de bruits blancs ( cas des n bruits blancs associés à chaque état) 
S
bb = Cov[b(i), b(j)] = B(i).dij dij = 0 si i Ļ j et dij = 1 si i = jS
bb= = B(i).dij
= B(i).dij
Modèle discret ou obtenu par discrétisation , il possède m entrées, s sorties et n états.

Equations du processus stochastique : ![]()
![]() la moyenne de X
la moyenne de X
![]() la covariance de líétat
la covariance de líétat
W(i) le bruit díétat, blanc et centré
![]() la covariance du bruit díétat
la covariance du bruit díétat
V(i) le bruit de mesure, blanc et centré
![]() la covariance du bruit díétat
la covariance du bruit díétat
![]() les bruits díétat et de mesure sont non-corrélés
les bruits díétat et de mesure sont non-corrélés
![]() les états et les bruits de mesure sont non-corrélés
les états et les bruits de mesure sont non-corrélés
![]() líétat initial et les bruits díétat sont non-corrélés
líétat initial et les bruits díétat sont non-corrélés
On montrerait comme dans le cas continu que le processus stochastique discret est líassociation díun processus stochastique de mesure et díun processus markovien.
On rappelle le problème résolu par le filtre de Kalman ; líestimation optimale des états X(i) díun système dynamique soumis à des entrées déterministes et aléatoires à partir de mesures bruitées Y(l), Y(l-1) , Y(-• ) passées et présentes. Líestimation est optimale au sens díun critère quadratique. Le critère est la minimisation de líerreur díestimation :
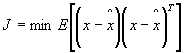
Les estimations sont linéaires vis à vis des mesures.
Notations
:![]() : estimation de líétat xi sachant les mesures yl , yl-1 , Ö, y-• effectuées.
: estimation de líétat xi sachant les mesures yl , yl-1 , Ö, y-• effectuées.
![]() : erreur díestimation de líétat xi sachant les mesures yl , yl-1 , Ö, y-• effectuées.
: erreur díestimation de líétat xi sachant les mesures yl , yl-1 , Ö, y-• effectuées.
![]() : la variance de líerreur díestimation de líétat xi sachant les mesures yl , yl-1 , Ö, y-• effectuées.
: la variance de líerreur díestimation de líétat xi sachant les mesures yl , yl-1 , Ö, y-• effectuées.
Le système est décrit par : ![]() est observable
est observable
Le modèle quíon en a établi : 
Le filtre de Kalman procède en deux étapes pour estimer au mieux líétat xi+1.
Première étape
: Après la ième mesure, on suppose que líon dispose díune estimation optimaleSeconde étape
: A líinstant i+1 on procède à la mesure de yi+1 ( également bruitée ), on compare cette mesure avec la prédictionOn cherche ![]() la meilleure estimation de xi+1 sachant les mesures y(i), Ö, y(-• ). On envisage les cas suivants où la commande est choisie égale à zéro pour simplifier l'étude.
la meilleure estimation de xi+1 sachant les mesures y(i), Ö, y(-• ). On envisage les cas suivants où la commande est choisie égale à zéro pour simplifier l'étude.
1į cas
:Líestimation de líétat xi est parfaite Þ ![]()
Il níy a pas de bruit díétat Þ Wi = 0
Þ
erreur díestimation :Il est inutile de procéder à la mesure de yi+1 sinon à ajouter des erreurs.
On choisit pour líestimation ![]()
2į cas
:Líestimation de líétat xi est parfaite Þ ![]()
état bruité wi Ļ 0
Þ
erreur díestimation :
3į cas
:Líestimation de líétat xi est imparfaite Þ ![]()
état bruité wi Ļ 0
Þ
erreur díestimation a priori :
![]() Interprétation géométrique de la prédiction
Interprétation géométrique de la prédiction
La meilleure prédiction ![]() de líétat xi+1 est celle qui minimise le carré de líerreur de prédiction :
de líétat xi+1 est celle qui minimise le carré de líerreur de prédiction : ![]() . Ce qui revient à minimiser la distance
. Ce qui revient à minimiser la distance ![]() , xi+1. Cíest donc la projection orthogonale de xi+1 sur le sous espace vectoriel
, xi+1. Cíest donc la projection orthogonale de xi+1 sur le sous espace vectoriel ![]() des estimations obtenues par filtrage linéaire ( i.e. combinaison linéaire ) des mesures y(i) , y(i-1), Ö, y(-• ).
des estimations obtenues par filtrage linéaire ( i.e. combinaison linéaire ) des mesures y(i) , y(i-1), Ö, y(-• ).
Remarque 1: líindice ns indique que les n états estimés sont une combinaison linéaire des s mesures.
Remarque 2 : Líespace vectoriel Hn est líespace vectoriel des signaux de puissance finie encore appelé L≤, il est muni du produit scalaire ( hilbertien ).
Remarques sur la prédiction
Si pour une raison quelconque on ne dispose plus des mesures, on peut à partir de la dernière mesure prédire les états futurs. Le problème de la prédiction est complètement déterministe.

Ce type de problème est rencontré par le mini-satellite HETE qui se positionne grâce au système GPS. Or ce récepteur ne peut être vu des satellites NAVSTAR que pendant 20 minutes alors que sa période de révolution est de 95 minutes. Le satellite doit prédire sa position pendant les 75 minutes restantes.
La prédiction a fourni ![]() telle que
telle que ![]() soit minimum. Líestimation consiste à exploiter la i+1 ème mesure pour affiner la prédiction.
soit minimum. Líestimation consiste à exploiter la i+1 ème mesure pour affiner la prédiction.

On cherche ![]() la meilleure estimation de xi+1 sachant les mesures y(i+1) , y(i), Ö, y(-• ). Ce qui équivaut à
la meilleure estimation de xi+1 sachant les mesures y(i+1) , y(i), Ö, y(-• ). Ce qui équivaut à ![]() soit minimum.
soit minimum.
![]() Comment la mesure peut-elle enrichir la connaissance de líétat xi+1 ?
Comment la mesure peut-elle enrichir la connaissance de líétat xi+1 ?
![]() et
et ![]()
De la i+1 ème mesure on tire : ![]()
La mesure nous renseigne sur líerreur de prédiction ![]() , au bruits de mesure près. Si la mesure est très bruitée, cette information présente peu díintérêt, il vaut mieux síen tenir à la prédiction.
, au bruits de mesure près. Si la mesure est très bruitée, cette information présente peu díintérêt, il vaut mieux síen tenir à la prédiction.

La mesure yi+1 et par suite líerreur de mesure ![]() enrichit le sous espace vectoriel des estimations
enrichit le sous espace vectoriel des estimations ![]() obtenues par filtrage des mesures yl , yl-1 , Ö, y-• du sous espace vectoriel
obtenues par filtrage des mesures yl , yl-1 , Ö, y-• du sous espace vectoriel ![]() . Soit
. Soit ![]() le nouveau sous espace vectoriel des estimations obtenues après filtrage des mesures passées et présentes. Líestimation
le nouveau sous espace vectoriel des estimations obtenues après filtrage des mesures passées et présentes. Líestimation ![]() qui minimise líerreur díestimation
qui minimise líerreur díestimation ![]() est la projection orthogonale de xi+1 sur le sous espace vectoriel
est la projection orthogonale de xi+1 sur le sous espace vectoriel ![]() .
.
ð
Cíest la projection orthogonale de xi+1 surð
Cíest la projection orthogonale de xi+1 sur![]() prédiction de líétat
prédiction de líétat
![]() variance de líerreur de prédiction
variance de líerreur de prédiction
![]() gain de Kalman
gain de Kalman
![]() estimation de líétat
estimation de líétat
![]() variance de líerreur díestimation
variance de líerreur díestimation
Ces équations sont à itèrer avec les conditions initiales :
![]() : état initial estimé,
: état initial estimé,
![]() : variance initiale de líerreur de prédiction.
: variance initiale de líerreur de prédiction.
Ces grandeurs traduisent la connaissance que líon a a priori du système.
![]() Interprétation des équations de Kalman
Interprétation des équations de Kalman
|
estimation = prédiction + innovation |
![]()
![]() Algorithme du filtre de Kalman
Algorithme du filtre de Kalman
|
|
Il est nécessaire de valider les estimations ; en effet, le filtre de Kalman étant récursif, un biais peut par exemple être à líorigine díune divergence du filtre. On se souvient quíon seulement accés aux mesures :

matrice (s * s) dont les termes diagonaux skk(i+1|i) ( où k Î [1,s] ) sont les variances des erreurs de mesure.
Dans le gas Gaussien, pour quíune variable aléatoire ait une probabilité de 99 % díappartenir à un domaine, il faut que cette variable aléatoire soit comprise dans un domaine de +/-3s autour de sa moyenne. Comme líestimateur est non biaisé ![]() , le test de divergence vérifie pour la kième mesure k Î [ 1 , s ] à líinstant i+1 que
, le test de divergence vérifie pour la kième mesure k Î [ 1 , s ] à líinstant i+1 que ![]() .
.
![]() Implantation du filtre de Kalman
Implantation du filtre de Kalman
La difficulté díimplantation du filtre de Kalman sur un calculateur réside dans le volume de calculs à traiter à chaque étape ( il síagit de calculs matriciels ! ). La commercialisation de processeurs de signaux bons marché est très récente ; ainsi jusquíà présent líemploi du filtre de Kalman était dédié aux applications très spécialisées (aéronautique, technologies spatiales Ö). On peut néanmoins proposer quelques améliorations visant à limiter le volume de calculs.
Ce gain ne dépend pas des mesures, il est donc possible de le calculer avant de démarrer le système ( off-line).
![]()
![]() Exemple d'application : Estimation de l'attitude d'un satellite de la famille SPOT
Exemple d'application : Estimation de l'attitude d'un satellite de la famille SPOT
La restitution d'attitude a pour données les informations fournies par les capteurs :
ę
Senseur d'acquisition terrestre ( STD ) fournit les angles de tangage q et de roulis f.
ę
Senseur d'acquisition solaire ( SSD ) fournit l'angle de lacet y.ę
Des gyromètres fournissent le vecteur rotation instantanée absolue ( par rapport au repère inertiel ).La mesure gyrométrique fournit une estimation de l'erreur d'attitude mais qui nécessite d'être recalée à long terme à cause de la dérive des gyromètres. Les mesures gyromètriques sont prélevées à la cadence de 8 hertz.
Le recalage est réalisé à partir des mesures fournies par les senseurs. à partir des mesures brutes de l'attitude ( senseurs SSD et STD. On procède au recalage à basse fréquence (moins de 1 hz ).

Pour de plus amples informations on se reportera à Technologies et techniques des véhicules spaciaux, tome 2 aux éditions Cèpaduès.