- Introduction
On a envisagé au chapitre 6 une technique de correction basée sur l’action proportionnelle qui vise à imposer aux système des performances dynamiques. On dispose d’un seul degré de liberté ( action sur K ) ce qui limite les performances du système à commander. On propose dans ce chapitre une approche polynomiale dans laquelle le système commandé doit suivre un modèle de référence défini par une fonction de transfert Hm(z). Les performances statiques et dynamiques souhaitées sont obtenues par le dimensionnement ad hoc
- Méthode de placement de pôles
Cette méthode permet, grâce à des abaques, d'obtenir assez rapidement des résultats satisfaisants à partir des spécifications temporelles liées à la réponse indicielle du système corrigé.
- Objectif :
Il s'agit d'obtenir un système par C(z) dont la FTBF corrigée possède les caractéristiques suivantes :
- un coefficient d'amortissement x pour le mode dominant
- une erreur maximale en régime permanent (pour la réponse indicielle)
- un dépassement D1 et un temps de pic tP

On notera : 
La FTBF vaut donc : 
D'où 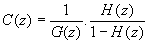
En se fixant a priori la dynamique du système corrigé, qui nous donnera les coefficients de H(z), on peut donc en déduire le correcteur C(z).
En notant  et
et 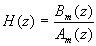 , on trouve :
, on trouve : 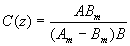
En pratique, il faudra d'assurer que ce correcteur est stable et bien sûr réalisable, ce qui va imposer des conditions sur le degré de son numérateur et de son dénominateur.
- Stabilité :
- les racines de
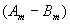 sont à l'intérieur du cercle unité
sont à l'intérieur du cercle unité
- les racines de B extérieures au cercle unité sont aussi racines de

- Réalisabilité :
Bien souvent, on imposera que le système corrigé se comporte comme un second ordre dominant s'écrivant :
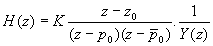
Y(z) est un polynôme dont les racines sont très proches de zéro, et qui ne sert qu'à assurer la réalisabilité de C(z), en permettant la vérification des relations écrites ci-dessus.
Dans la suite, on supposera que ces relations sont vérifiées et on prendra Y(z)=1.
Si on décide d'avoir une erreur nulle en régime permanent (réponse indicielle), cela implique :
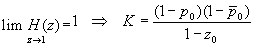
Démarche à suivre :
- Calculer G(z)
- Définir H(z) d'après le cahier des charges (D1, x, tP)
- assurer la réalisabilité de C(z)
- fixer z0 si G(z) possède un zéro instable
- A l'aide de la figure

, déterminer les valeurs possibles de g pour D1 et x imposés
- Reporter cet intervalle sur la figure
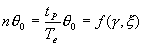 et en déduire l'intervalle correspondant à
et en déduire l'intervalle correspondant à 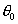 . En pratique, on prendra des valeurs faibles pour
. En pratique, on prendra des valeurs faibles pour 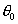
.
- Sur la figure , déterminer la position de p0 à l'intersection de la radiale
et de l'iso-x désiré
- construire l'angle g suivant la méthode indiquée sur la figure 1, puis :
- Si z0 est libre, en déduire la position de z0
- Si z0 est imposé, vérifier que g appartient à l'intervalle défini précédemment.
- Calculer C(z)

Figure 1
Figure 2
- Régulateur RST
- Structure du régulateur RST

Figure 3
Hypothèses :

- Système propre i.e. degré(A(z)) > degré(B(z)),
- A(z) monique i.e. dont le coefficient du terme de plus haut degré vaut 1
- A(z) et B(z) sont premiers entre eux i.e. qui ne possèdent aucun facteur commun
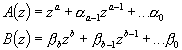
Le polynôme R(z) est monique de degré r,
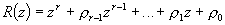
Le polynôme S(z) de degré s,
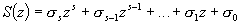
Le polynôme T(z) est monique de degré t,
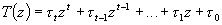
La fonction de transfert en boucle fermée :

La loi de commande à implanter sur le calculateur résulte de :

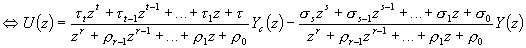
On applique le théorème de l'avance pour exprimer u(k+r) :
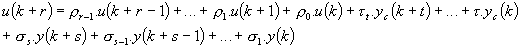
La sortie ne peut anticiper l'entrée, par conséquent :
- Synthèse du régulateur RST
On a établi : 
Les polynômes R(z), S(z) et T(z) vont être choisis afin que la fonction de transfert en boucle fermée soit identique à une fonction de transfert Hm(z) encore appelé modèle à poursuivre.
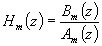 Système propre i.e. degré(Am(z)) > degré(Bm(z)). De plus les pôles de Hm(z) sont tous stables donc à l'intérieur du cercle unité. Ces pôles sont placés afin de maîtriser le régime transitoire en boucle fermée ; de plus le degré de Am(z) n'est pas nécessairement égal à celui de A(z).R(z) + B(z).S(z). Am(z) étant généralement un modèle à poursuivre très simple, son degré est la plupart du temps nettement inférieur à celui de A(z).R(z) + B(z).S(z). Avec un régulateur RST on dispose donc de deux degrés de liberté pour le réglage de la dynamique ( R(z) et S(z) ).
Système propre i.e. degré(Am(z)) > degré(Bm(z)). De plus les pôles de Hm(z) sont tous stables donc à l'intérieur du cercle unité. Ces pôles sont placés afin de maîtriser le régime transitoire en boucle fermée ; de plus le degré de Am(z) n'est pas nécessairement égal à celui de A(z).R(z) + B(z).S(z). Am(z) étant généralement un modèle à poursuivre très simple, son degré est la plupart du temps nettement inférieur à celui de A(z).R(z) + B(z).S(z). Avec un régulateur RST on dispose donc de deux degrés de liberté pour le réglage de la dynamique ( R(z) et S(z) ).
- Réglage de la précision
L'annulation de l'erreur permanente est conditionnée par le nombre d'intégrations dans la chaîne directe. Pour une entrée type complexe de la forme  , il convient d'insérer l intégrations dans la chaîne directe ; on écrit :
, il convient d'insérer l intégrations dans la chaîne directe ; on écrit :

- Simplification de zéros
La fonction de transfert en boucle fermée du processus corrigé  est généralement d'ordre supérieur au modèle à poursuivre
est généralement d'ordre supérieur au modèle à poursuivre 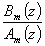 . Il existe donc des simplifications qui seront obtenues à l'aide des polynômes R(z), S(z) et T(z).
. Il existe donc des simplifications qui seront obtenues à l'aide des polynômes R(z), S(z) et T(z).
Le processus à commander H(z) possède b zéros qui sont les racines de B(z). Ces zéros conditionnent le régime transitoire. On distingue :
- Les zéros compensables, z+ racines du polynôme B+(z) choisi monique. Les zéros compensables appartiennent à la zone hachurée de la figure 2, ils garantissent un amortissement sûr et rapide des modes. Cette zone doit être choisie en fonction du cahier des charges. Elle sera définie par
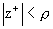 et
et  , les valeurs de r et x0 dépendant du type de zéros qu'on voudra compenser.
, les valeurs de r et x0 dépendant du type de zéros qu'on voudra compenser.
- Les zéros non compensables, z- racines du polynôme B-(z), Les zéros non compensables sont exclus du contour hachuré.

Figure 4
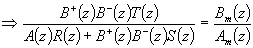
Comme B+(z) est compensable, R(z) contient B+(z) Þ  et R'(z) est monique car B+(z) et R(z) le sont.
et R'(z) est monique car B+(z) et R(z) le sont.
Comme B-(z) n'est pas compensable, Bm(z) contient B-(z) Þ 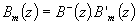
Pour le choix de T, on peut écrire :
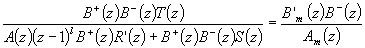
Þ
A(z).(z-1)l.R'(z) + B-(z).S(z) = Am(z).A0(z) à un facteur A0(z) près compte tenu de la remarque du début de paragraphe portant sur les degrés du processus bouclé corrigé et du modèle à poursuivre.
Þ
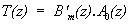 égalité vérifiée au même polynôme A0(z) près.
égalité vérifiée au même polynôme A0(z) près.
On démontre en annexe que :

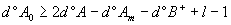


Synthèse
|
Données
A(z) et B(z) premiers entre eux |
|
Spécifications
Le cahier des charges permet d'exprimer Am(z) et éventuellement Bm(z) |
|
Etape 1
 qui donne dBm qui donne dBm
|
|
Etape 2
Effectuer la factorisation B(z) = B+(z). B-(z), les zéros de B+(z) appartenant à la zone tramée de la figure 4 |
|
Etape 3
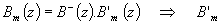
|
|
Etape 4
Déterminer l le nombre d'intégrations à rajouter dans la boucle ouverte |
|
Etape 5
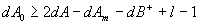
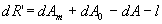

|
|
Etape 6
Résoudre A(z).(z-1)l .R’(z) + B-(z).S-(z) = A0(z)Am(z) |
|
Etape 7
Calculer R(z) = B+(z). (z-1)l .R’(z) et T(z) = B’m(z).A0(z) |
- Exemple
On veut corriger un processus du second ordre trop faiblement amorti (x = 0,2) et de pulsation propre wn = 0,7 rad/s. Son gain statique est égal à 1.
On désire avoir un système mieux amorti (x = 0,8) avec une erreur statique nulle. On désire aussi compenser seulement les zéros se trouvant dans la zone définie par x < 0,3.
On peut espérer doubler la pulsation propre : w'n = 1,4 rad/s. On prendra un temps d'échantillonnage 
Ecrivons d'abord la transmittance du processus non corrigé grâce aux abaques du chapitre IV :
Pour w'n.Te = 1, on a wn.Te = 0,5 donc on trouve :
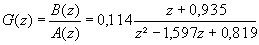
B(z) possède un zéro non compensable z0 = -0,935 (il se trouve en dehors du domaine).
On écrit donc B-(z) = 0,114.(z + 0,935) et B+(z) = 1
Ecrivons maintenant la FTBF du système corrigé en fonction du cahier des charges :
 avec
avec 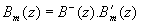
de plus 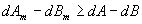 = 1 donc
= 1 donc 
Comme dB- = 1, on va donc prendre B'm(z) = K
K va nous permettre de régler le gain statique et de respecter la contrainte liée à la précision.
On veut x = 0,8 et w'n = 1,4 rad/s, on en déduit les pôles de H(z) : 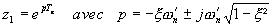
Comme 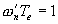 ,
, 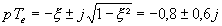
D'où 

finalement 
On veut une erreur statique nulle, il faut donc avoir une intégration dans la boucle ouverte, d'où l = 1
 = 4 – 2 – 0 + 1 – 1 = 2
= 4 – 2 – 0 + 1 – 1 = 2
on prend A0 = z² (on choisira toujours A0 le plus simple possible)
 = 1
= 1
et  = 2
= 2
d'où R'(z) = z+r0 et S(z) = s2.z² + s1.z + s0
On résout par identification l'équation 

On trouve le système d'équations suivant :

Finalement :
R(z) = z² - 0,315z - 0,685 S(z) = 10,284z² – 13,459z+5,26 T(z) = 2,085z²
Réponse indicielle
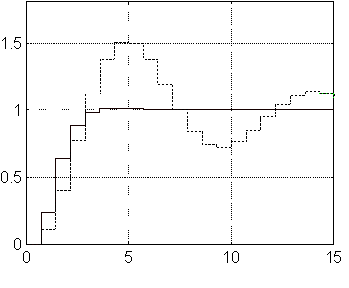

![]()
![]()
![]()
![]() et
et ![]() , on trouve :
, on trouve : ![]()





