dont la transformée en z s’écrit : L’équivalent de l’intégration continue pour les systèmes causals échantillonnés a pour expression :
dont la transformée en z s’écrit :
On remarquera qu’une intégration équivaut à un système du premier ordre de pôle égal à 1.
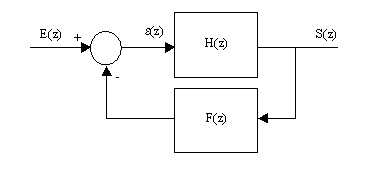
La fonction de transfert en boucle ouverte FTBO(z) = F(z).H(z) possède k intégrations, un tel système est dit de classe k ( cf asservissements linéaires continus chapitre 6 ) peut s’écrire :
L’erreur e(z) a pour expression : 
En régime permanent : 
L’expression de l’erreur est fonction de la nature de l’entrée E(z), c’est ce que montre le tableau suivant :
|
|
|
|
|
|
k=0 |
|
|
¥ |
|
k=1 |
0 |
|
¥ |
|
k=2 |
0 |
0 |
|
Remarque : Dans le cas général , une entrée peut s’écrire comme la superposition d’entrées types élémentaires ( échelon, rampe, rampe d’accélération etc.). E(z) a pour expression :
