- Conditions générales de stabilité
Comme pour les systèmes linéaires continus, on définit la stabilité d'un système linéaire échantillonné par sa capacité à revenir à son état initial après avoir été excité par une perturbation.
Prenons un système défini par la séquence de réponse impulsionnelle {hn}, il est stable si hn ® 0 lorsque n® +∞.
Si la transmittance d'un système échantillonné (qui est aussi la transformée en z de sa réponse impulsionnelle) peut s'écrire sous la forme :
 avec deg(N(z)) = n £ d
avec deg(N(z)) = n £ d
on peut la décomposer en éléments simples : 
Pour que la réponse impulsionnelle tende vers 0 quand n® +∞, il faut que chacun des termes qui la composent tende aussi vers 0.
La transformée inverse de H(z) nous donne alors : 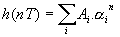
Ce terme ne tend vers zéro que si  a un module inférieur à 1.
a un module inférieur à 1.
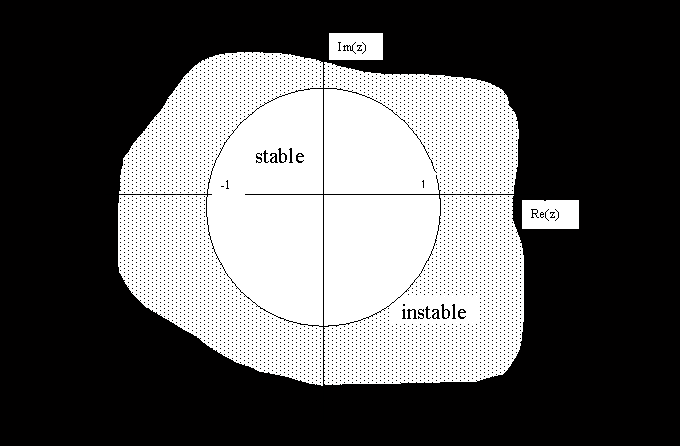
La condition de stabilité pour un système linéaire échantillonné est que toutes les racines de l'équation caractéristique (pôles de transmittance) soient situées à l'intérieur du cercle unité du plan des z.
On avait posé dans le chapitre 2 : 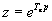 .
.
En écrivant p = s +jw , la condition de stabilité s'écrit  ce qui équivaut à s < 0.
ce qui équivaut à s < 0.
On retrouve le résultat obtenu pour les systèmes continus.
- Critères algébriques de stabilité
- Critère simplifié de Jury
Soit D(z) le dénominateur de la transmittance H(z) d'un processus.
L'équation 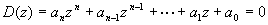 avec
avec  permet de déterminer les pôles de H(z).
permet de déterminer les pôles de H(z).
Dans le cas où n > 2, il est généralement difficile de calculer ces pôles "à la main". C'est pourquoi on utilise une méthode fondée sur la construction du tableau ci-dessous :
N° de ligne
|
1 |
a0 |
a1 |
a2 |
… |
ak |
… |
an-k |
… |
an-2 |
an-1 |
an |
|
2 |
an |
an-1 |
an-2 |
… |
an |
… |
ak |
… |
a2 |
a1 |
a0 |
|
3 |
b0 |
b1 |
b2 |
… |
bk |
… |
bn-k |
… |
bn-2 |
bn-1 |
|
|
4 |
bn-1 |
bn-2 |
bn-3 |
… |
bn-1-k |
… |
bk-1 |
… |
b1 |
b0 |
|
|
5 |
c0 |
c1 |
c2 |
… |
ck |
… |
cn-k |
… |
cn-2 |
|
|
|
6 |
cn-2 |
cn-3 |
… |
… |
cn-2-k |
… |
ck-2 |
… |
c0 |
|
|
|
. |
. |
. |
. |
. |
. |
. |
. |
|
|
|
|
|
. |
. |
. |
. |
. |
. |
. |
. |
|
|
|
|
|
. |
. |
. |
. |
. |
. |
. |
. |
|
|
|
|
|
. |
. |
. |
. |
. |
. |
. |
. |
|
|
|
|
|
2n-5 |
p0 |
p1 |
p2 |
p3 |
|
|
|
|
|
|
|
|
2n-4 |
p3 |
p2 |
p1 |
p0 |
|
|
|
|
|
|
|
|
2n-3 |
q0 |
q1 |
q2 |
|
|
|
|
|
|
|
|
bk = a0ak - anan-k
ck = b0bk - bn-1bn-1-k etc…
Le tableau s'arrête lorsqu'il ne reste plus que 3 éléments.
Critère de Jury (1961):
Pour que toutes les racines de D(z) soient dans le cercle unité, il faut et il suffit que les conditions suivantes soient satisfaites :
- D(1) > 0 " n
- D(-1) > 0 si n pair
D(-1) < 0 si n impair
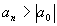

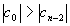


Exemple : 
Construisons le tableau :
N° de ligne
|
1 |
a0 |
a1 |
a2 |
a3 |
|
2 |
a3 |
a2 |
a1 |
a0 |
|
3 |

|

|
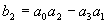
|
|
Les conditions de stabilité sont alors :
- D(1) > 0 Û a3+a2+a1+a0 = 0
- D(-1) < 0 Û -a3+a2-a1+a0 = 0


- Critère de Routh modifié
On peut se ramener au critère de Routh étudié lors du cours d'asservissements linéaires continus en effectuant le changement de variables suivant :
 , si p.Te << 1
, si p.Te << 1 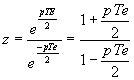 , posons
, posons 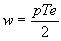

où w est un nombre complexe qu'on peut écrire  .
.
De là, 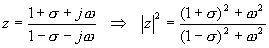
On en déduit : 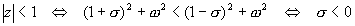
Autrement dit, si l'on transforme D(z) en D(w) en posant  , le système est stable si les racines de D(w) = 0 sont à partie réelle strictement négative. On peut donc appliquer le critère de Routh sur les coefficients de D(w).
, le système est stable si les racines de D(w) = 0 sont à partie réelle strictement négative. On peut donc appliquer le critère de Routh sur les coefficients de D(w).
- Critère graphique : lieu d'Evans
- Principe
Le principe du lieu d'Evans est identique à ce qui a été dit pour les systèmes continus. Il s'agit de représenter l'ensemble des pôles de la FTBF d'un système linéaire échantillonné en fonction d'un paramètre k placé dans la chaîne directe, comme indiqué sur le schéma ci-dessous:


Les pôles de la FTBF sont les racines de l'équation 1+kG(z) = 0
Le système sera stable si ces pôles sont situés à l'intérieur du cercle unité dans le plan des z.
- Règles de construction
Les règles de construction du lieu d'Evans sont similaires à celles énoncées lors du cours d'asservissements linéaires continus.
Si k > 0 : Si k < 0 :


On note zi les m zéros et pi les n pôles de G(z).
Attention ! Les pôles de G(z) s'écrivent bien en z et non en p, comme la notation pourrait le laisser penser.
- Points de départ : les n pôles de G(z)
- Points d'arrivée : les m zéros de G(z) et les n-m directions asymptotiques
- Asymptotes : elles font un angle avec l'axe réel

si k > 0
Elles concourent au point 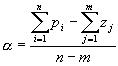
- Parties du lieu sur l'axe réel :
Si k > 0, un point de l'axe réel appartient au lieu s'il laisse à sa droite un nombre impair de pôles et de zéros, comptés avec leur ordre de multiplicité.
Si k < 0, un point de l'axe réel appartient au lieu s'il laisse à sa droite un nombre pair de pôles et de zéros, comptés avec leur ordre de multiplicité.
- Points de branchement : ce sont les points où les branches du lieu se détachent de l'axe réel.
Ils correspondent à des racines doubles du lieu et vérifient :
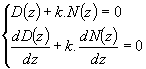 avec z réel et appartenant au lieu,
avec z réel et appartenant au lieu,
soit encore 
On peut également trouver leur abscisse b par la relation :


- Points d'intersection avec l'axe imaginaire : on pose z = jw
D'où 

- Exemple

T = 1 s

pour T = 1 s,  puisque
puisque 
La FTBF vaut 
Construction du lieu d'Evans :
- Normalisation du gain : k = 0,37K
- Points de départ : p1 = 1 p2 = 0,37
- Points d'arrivée : z1 = -0,7
- Asymptote :
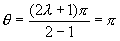
- Parties de l'axe réel :
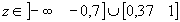
- Points de branchement :


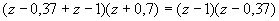
d'où z = 0,65 ou z = -2,05
- Equation du lieu :
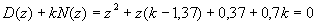
On pose z = x +jy :
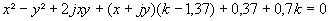
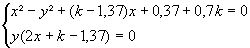
On a donc une partie de l'axe réel (y = 0), résultat déjà connu.
D'autre part, k = 1,37 – 2x
que l'on reporte dans l'autre équation

On obtient un cercle de centre (-0,7 ; 0) et de rayon 1,35 (cela confirme les points de branchement trouvés précédemment).
- Intersection du lieu avec le cercle unité :
Pour déterminer le k maximal de stabilité, on pose le système d'équations :
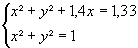
on trouve x = 0,235 d'où klim = 1,37 – 2x = 0,9
comme k = 0,37K, on a finalement Klim = 2,43

Remarque : Comme dans le cas continu il est possible d’imposer au système un comportement de type second ordre en s’imposant le facteur d’amortissement réduit x et la pulsation propre non amortie wn. On trace dans le plan complexe les isox et les isown .
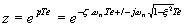
w
n.Te varie, x constant pour le tracé des isox ,
x
varie, wn.Te constant pour le tracé des isown.Te

 avec deg(N(z)) = n £ d
avec deg(N(z)) = n £ d![]()
![]()
![]() a un module inférieur à 1.
a un module inférieur à 1.
![]() .
.![]() ce qui équivaut à s < 0.
ce qui équivaut à s < 0.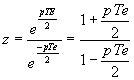 , posons
, posons 


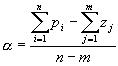
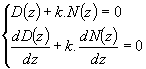 avec z réel et appartenant au lieu,
avec z réel et appartenant au lieu,


