On cherche à établir une relation d'entrée sortie pour un système échantillonné. Dans un premier temps, il paraît naturel de l'établir dans le domaine temporel.
Figure 1
On soumet ce processus continu, linéaire, invariant à une impulsion et on observe la réponse impulsionnelle notée h:
On soumet ce même processus à une impulsion décalée, par invariance du système :
Pratiquement l'entrée est la somme d'impulsions retardées, pondérées par e.
Chaque impulsion pondérée par e agit pour son propre compte au travers du système ( le système étant linéaire, on peut appliquer le théorème de superposition ).
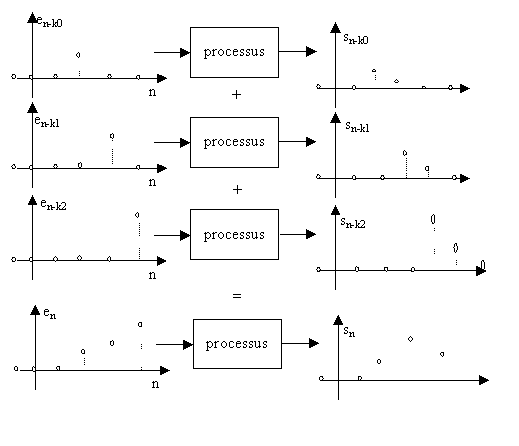
La réponse apparaît comme étant un produit de convolution discret :
Plutôt que de manipuler un produit de convolution dans le domaine temporel, on montre en cherchant les transformées en Z de e, s et h notées respectivement E(z), S(z) et H(z) que :
Les systèmes continus, linéaires, invariants peuvent être décrits par des équations différentielles linéaires à coefficients constants. D'une manière analogue, les systèmes échantillonnés sont décrits par des équations de récurrence.
On applique le théorème de l'avance, les conditions initiales étant toutes nulles :
La fonction de transfert en z : 
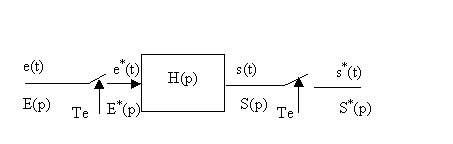
Or, 
d'après ce qui précède sur la convolution.
Donc
En pratique, deux cas sont à distinguer selon qu'il y a ou non des échantillonneurs entre les blocs.
Il n'y a pas par exemple pas d'échantillonneur lorsque l'on a affaire à un capteur délivrant une information analogique ( génératrice tachymétrique, thermocouple etc.). Dans cel cas la sortie du processus est connectée directement au capteur. Il faut calculer la fonction de transfert de l'ensemble { processus + capteur }.
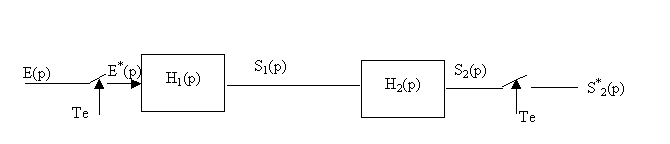
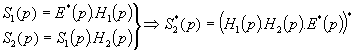
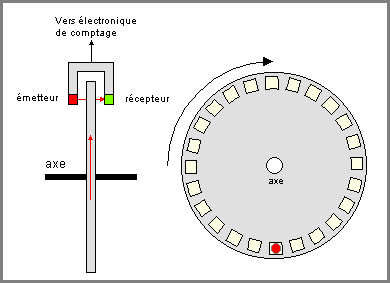
Il y a échantillonnage "naturel" de la mesure lorsqu'on utilise un capteur numérique ( codeur optique incrémental ou absolu ).
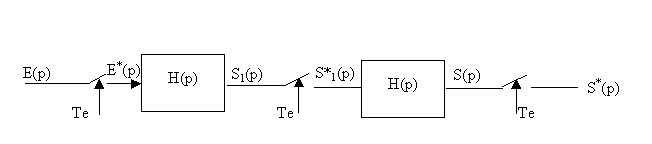
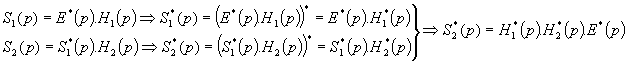
Le bloqueur d'ordre 0 maintient sa sortie constante pendant toute la période d'échantillonnage. Pour déterminer sa fonction de transfert on applique à son entrée une impulsion.
En effet, la réponse impulsionnelle est égale à la fonction de transfert ( Cf. Asservissements linéaires continus chapitre 2 ). La fonction de transfert du bloqueur d'ordre zéro s'écrit d'après le théorème du retard :
La fonction de transfert échantillonnée du système continu muni de son bloqueur d'ordre zéro a alors pour expression :
On a établi au chapitre 2 que : 
, la fonction de transfert en z du système continu muni de son bloqueur d'ordre zéro a pour expression :
Deux cas sont à discuter selon la nature du capteur employé, analogique ou numérique.
La sortie y du processus est mesurée, filtrée ( antirepliement ) puis échantillonnée.
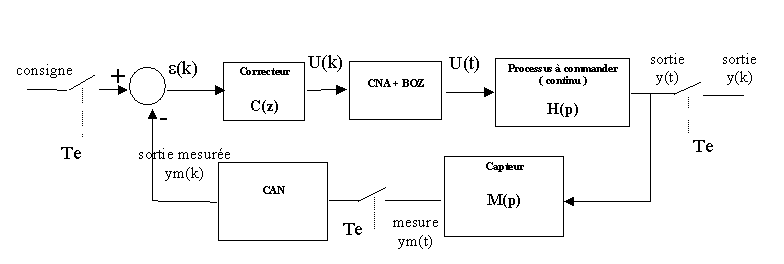
On calcule dans un premier temps la fonction de transfert en boucle ouverte, il faudra considérer globalement le système et la chaîne de mesure.
La fonction de transfert en boucle fermée : 
en considérant un échantillonnage fictif de y(t).
(1)
(2)
(2) à (1) 
De par sa technologie, le capteur restitue une mesure discrétisée de la sortie . Il n'est pas nécessaire de filtrer et d'échantillonner la mesure.
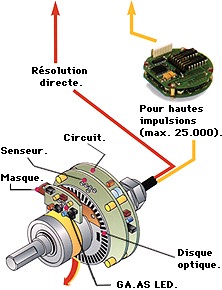
On calcule dans un premier temps la fonction de transfert en boucle ouverte, il faudra considérer séparémment le système et la chaîne de mesure.
La fonction de transfert en boucle fermée : en considérant l'échantillonnage fictif de y(t).
