3-2 Amortisseur de tangage :
a - Equations :
On rappelle que sous les hypothèses émises pour effectuer cette étude (en particulier découplage des modes oscillation d'incidence et oscillation phugoïde) les équations sont:
![]()
La représentation d'état associée est donc:
![]()
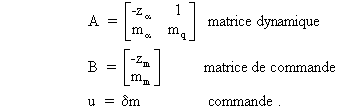
Remarque:
si à partir de cette représentation on calcule l'équation caractéristique du système, on trouve:
![]()
La représentation schématique du système est:
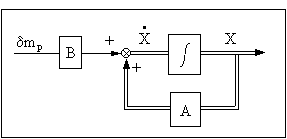
Mettre en oeuvre un retour d'état pour modifier les caractéristiques du système se traduit par:
- au niveau des équations:
avec
et
- au niveau du schéma:
b - Réglage :
Le but premier du correcteur d'état est d'augmenter l'amortissement du mode pseudo-périodique. L'effet prépondérant pour obtenir ce résultat viendra (comme dans le cas de l'amortisseur de tangage classique) du coefficient Kq du correcteur K (retour tachymétrique). Le deuxième terme du correcteur offre un degré de liberté supplémentaire qui permet d'éviter l'inconvénient rencontré au chapitre 3 concernant le gain statique de la vitesse de tangage.
Pour effectuer ce réglage, on s'impose donc a priori l'amortissement xAT et le gain statique que l'on désire.
On sait que le gain statique concernant la vitesse de tangage de l'avion naturel est (voir chapitre 3):
![]()
Il nous faut donc maintenant trouver le gain statique de la
vitesse de tangage de l'avion corrigé. Une méthode pour y
parvenir est de calculer la fonction de transfert ![]() . Dans ce cas, on
considère que la sortie du système est q. Donc, pour la
deuxième équation de la représentation d'état, il faut
prendre C = [ 0 1 ]. On a ainsi:
. Dans ce cas, on
considère que la sortie du système est q. Donc, pour la
deuxième équation de la représentation d'état, il faut
prendre C = [ 0 1 ]. On a ainsi:
![]()
Le calcul de cette équation donne:
![]()
Le dénominateur s'écrit:
![]()
Pour répondre au critère de gain statique il faut donc écrire:
![]()
D'où on déduit:
![]()
Il reste alors à résoudre le système de deux équations à deux inconnues suivant:
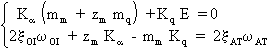
dans lequel les inconnues sont Ka,
et Kq puisque l'on se donne xAT, et que ![]() .
.