2-2 Calcul du correcteur :

Le problème posé peut se décomposer en deux étapes successives:

 Trouver, calculer ou s'imposer la dynamique du système corrigé,

‚ Calculer le correcteur K permettant d'obtenir ce résultat.

 Dynamique du système corrigé:

Il existe plusieurs méthodes permettant de fixer au système corrigé un comportement ou une dynamique:

- Le placement de pôles,

- la méthode "SFENA",

- La méthode de "Naslin" développée dans ce polycopié,

- .....

Elles ont toutes le même but; celui de permettre de calculer les coefficients correspondant à une dynamique en boucle fermée.

‚ Calcul du correcteur:

Le calcul du correcteur permettant d'obtenir la dynamique désirée (matrice ) à partir de la dynamique du système libre (matrice A) est très aisé dès lors que ce calcul est effectué dans la base où les matrices A et sont sous forme compagne horizontale.

Considérons un système dont la représentation est en base compagne horizontale:

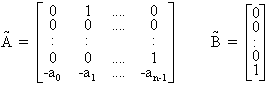
Son équation caractéristique est:

Si on se donne l'équation caractéristique en boucle fermée suivante:

La représentation sous forme compagne horizontale du système corrigé est:

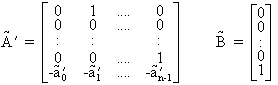
Si on note le correcteur à appliquer dans la base compagne horizontale, on a à partir de la relation établie plus haut:

Le calcul de donne:

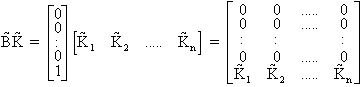
On obtient alors:

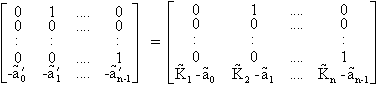
Par identification, on trouve alors la relation remarquable:

Le correcteur trouvé est applicable dans la base compagne horizontale. Dans la base avion, il faut appliquer le correcteur calculé à partir des formules de changement de base donnée en annexe 6. Pour le correcteur on a: