4-2 Tenue de pente :

La vitesse étant supposée constante, on a pour les paramètres du modèle avion:

a - Loi de pilotage :

Le pilote automatique doit élaborer, pour cette fonction, un ordre de braquage de gouverne qui soit linéaire, et qui amène la pente réelle de l'avion (pente mesurée) à la valeur de la pente consigne imposée par le pilote.

Il faut donc, si un écart existe entre la pente consigne et la pente mesurée élaborer un braquage consigne de la gouverne de profondeur tendant à annuler l'écart.

Si > , puisqu'il s'agit de variations, il faut imposer à l'avion un ordre "à piquer" donc un > 0 .
Si < , il faut imposer à l'avion un ordre "à cabrer" donc un < 0 .
Si = , il faut imposer à l'avion un ordre = 0 .

Si l'on adopte, comme dans le paragraphe précédent une commande proportionnelle à l'écart qui respecte ces critères, on prend:

Le gain permet d'assurer la stabilité du système s'il y a lieu, et de régler la rapidité du mode. Pour répondre au critère de signe liant , et , il faut prendre:

b - Schéma fonctionnel :

Dans le cas de la tenue d'assiette, on avait une relation simple entre q et q. Une telle relation n'existe pas entre g et q c'est pourquoi, dans le schéma fonctionnel ci-dessous, l'avion est représenté par deux fonctions de transfert: (puisque l'on conserve l'amortisseur de tangage).

La fonction de transfert de l'amortisseur de tangage est celle qui a été établie au chapitre précédent. Ici, le pilote n'est plus "aux commandes", donc l'entrée du sous-système "amortisseur" n'est plus l'ordre pilote dmp, mais la consigne de braquage "élaborée" par la loi de commande choisie dmc. On rappelle donc que, comme pour la tenue d'assiette, on a:

Si l'on suppose alors que le capteur de la pente est parfait (fonction de transfert unité), on a .

c - Fonctions de transfert :

Le gain permet de régler la tenue de pente (rapidité, précision, stabilité s'il y a lieu). Pour cela, il faut disposer des fonctions de transfert en boucle ouverte et en boucle fermée du système.

Calcul de la FTBO:

Par définition la FTBO s'écrit:

Que l'on peut mettre sous la forme: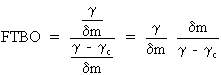

 Calcul de :

L'avion étant équipé d'une automanette supposée parfaite, les états V et sont nuls dans le modèle longitudinal. La première équation est donc sans signification et la dernière n'apporte aucune information utile. Dans ce cas, le modèle mathématique s'écrit:

On en déduit alors:

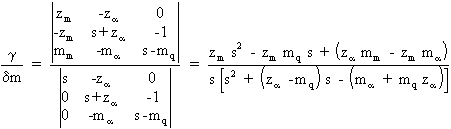
Donc:

Remarques:

- Ce résultat se retrouve très rapidement en mettant sous forme de représentation d'état les trois équations retenues pour la tenue de pente et en calculant la relation:

- On reconnaît au dénominateur de l'équation caractéristique de l'oscillation d'incidence.

‚ Calcul de :

Donc:

Et

Que l'on peut mettre sous la forme:

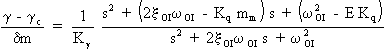
On en déduit donc l'expression de la fonction de transfert en boucle ouverte:

Calcul de la FTBF:

Par définition, la FTBF du système s'écrit:

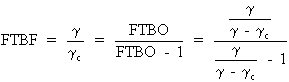
On a donc:

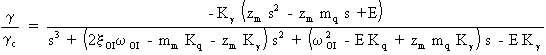
Remarque:

Le gain statique de est: