2-2 Tenue d'assiette :

La tenue d'assiette correspondant au pilotage de l'avion, seul le mode rapide de l'avion naturel (oscillation d'incidence) nous intéresse.

a - Loi de pilotage :

Le pilote automatique doit élaborer, pour cette fonction, un ordre de braquage de gouverne qui soit linéaire, et qui amène l'assiette réelle de l'avion (assiette mesurée) à la valeur de l'assiette consigne imposée par le pilote.

les calculs étant effectués sur le modèle avion établi au chapitre 2, on rappelle que l'ensemble des paramètres du modèle représentent les variations autour du point de vol équilibré étudié. Dans ce modèle, les seuls paramètres permettant de commander le système sont le braquage de la gouverne noté dm et la commande des gaz notée dt.

Si l'on indice les paramètres de la lettre "c" pour ceux qui concernent les consignes et de la lettre "m" pour ceux qui concernent les mesures, il faut donc, si un écart existe entre l'assiette consigne et l'assiette mesurée élaborer un braquage consigne de la gouverne de profondeur tendant à annuler l'écart.

Si > , puisqu'il s'agit de variations, il faut imposer à l'avion un ordre "à piquer" donc un > 0 .
Si < , il faut imposer à l'avion un ordre "à cabrer" donc un < 0 .
Si = , il faut imposer à l'avion un ordre = 0 .

De plus, il est intuitif d'imposer un ordre d'autant plus grand que l'écart est grand. Le type de loi le plus simple qui réponde à ces critères est une loi proportionnelle à l'écart. Elle s'écrit:

Le gain permet d'assurer la stabilité du système s'il y a lieu, et de régler la rapidité du mode. Pour répondre au critère de signe liant , et , il faut prendre:

b - Schéma fonctionnel :

L'amortisseur de tangage étant conservé, le schéma fonctionnel représentatif de la tenue d'assiette ainsi élaborée est donc le suivant:

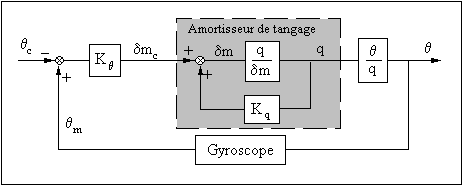
Il faut bien noter que, même si le pilote n'intervient plus ( en entrée de l'amortisseur de tangage), la fonction de transfert reliant q la vitesse de tangage de l'avion et est strictement la même que celle établie dans le chapitre précédent entre q et . On a donc:

avec

De plus, les équations cinématiques du modèle avion nous donnent:

donc:

Si l'on considère enfin que le gyroscope est parfait et donne une mesure exacte et instantanée (fonction de transfert unité), le schéma fonctionnel se simplifie de la manière suivante:

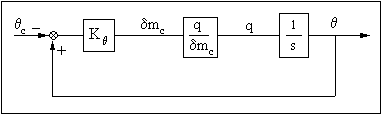
Remarque : Dans cette étude, on ne s'est intéressé qu'au mode naturel rapide de l'avion. On ne tient donc pas compte, pour simplifier les calculs, des variations de la vitesse; une étude plus poussée montrerait qu'en résolvant le système complet les performances pour un même point de vol sont modifiées.

c - Fonctions de transfert :

Le gain permet de régler la tenue d'assiette (rapidité, précision, stabilité s'il y a lieu). Pour cela, il faut disposer des fonctions de transfert en boucle ouverte et en boucle fermée du système.

Calcul de la FTBO:

Par définition, la FTBO du système est: . On a donc:

D'où

Calcul de la FTBF:

Par définition, la FTBF du système est: . Or:

La FTBF s'écrit donc:

Remarque:

Le gain statique de est: