4-4 Etude du modèle complet :

Si l'on excepte la dernière équation du modèle () qui est une intégration pure et ne modifie pas la dynamique des autres variables, il reste:

L'équation caractéristique du système ainsi défini est:

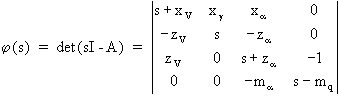
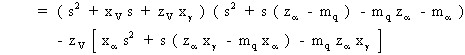
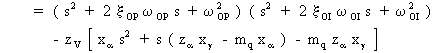
Si on compare les pôles de l'oscillation d'incidence, les pôles de l'oscillation phugoïde et les pôles de l'équation caractéristique, on remarque que:

sont proches des pôles de l'OI

sont proches des pôles de l'OP

La mise en place dans le plan complexe de ces pôles donne:

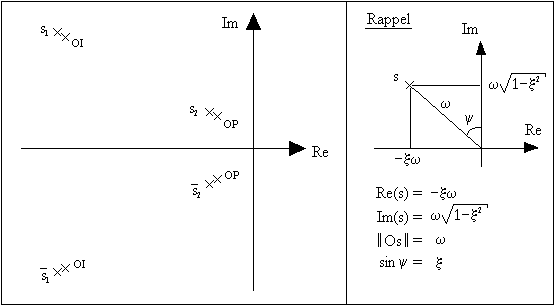
On peut donc dire que le mouvement complet de l'avion, qui est la superposition des deux modes, peut être considéré comme la succession de ces deux modes.

On a donc découplage des modes longitudinaux. Le calcul des caractéristiques effectué en utilisant les systèmes réduits d'équations, comme fait aux paragraphes 4-3-a et 4-3-b est donc valide.

On peut considérer ainsi que de l'instant t=0, instant initial du mouvement, à t= (temps de réponse de l'oscillation d'incidence) V et g n'ont pas encore évolué donc:

Et au-delà de l'instant t=, on peut considérer que l'incidence n'évolue plus et que seules V et g varient:

Sur le modèle complet de l'avion, cela revient à négliger les termes de couplage du système () entre les deux groupes d'équations. Dans ce cas, si on calcule l'équation caractéristique du système, on obtient:

Sur la modélisation de l'avion, en représentation d'état, ces termes de couplage apparaissent dans la matrice A:

Les négliger revient à écrire:

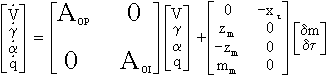
avec:

Exemple numérique:

On considère un avion dont les coefficients du modèle sont:

Calcul de l'équation caractéristique:

En reprenant l'expression de l'équation caractéristique trouvée plus haut on obtient:

Les racines de cette équation, et les caractéristiques correspondant sont regroupées dans le tableau ci-dessous:

Si on suppose que les modes sont découplés, on peut calculer, à partir des relations établies précédemment sous ces hypothèses, les équations caractéristiques des deux oscillations:

Oscillation d'incidence:

Oscillation phugoïde:

Les caractéristiques calculées sont alors:

Ces deux tableaux montrent que les résultats sont respectivement très proches les uns des autres.

De plus, , ce qui permet d'affirmer que le découplage est justifié.

Conclusion :

Le découplage est une approximation permettant le calcul des caractéristiques des modes propres de l'avion de manière simple.

Cependant, vues les hypothèses émises a priori, il faut, dans chaque cas, en vérifier la validité, en particulier grâce à la simulation.

Le modèle linéaire obtenu a une validité relativement large (ne pas oublier qu'il s'agit d'un modèle développé autour d'un point de vol équilibré), et il permet de retrouver les caractéristiques du mouvement de l'avion rigide comme on pourrait les avoir à partir des équations générales.

Si l'on veut tenir compte des modes dus à la souplesse de la structure de l'avion, il faut augmenter l'ordre du système.

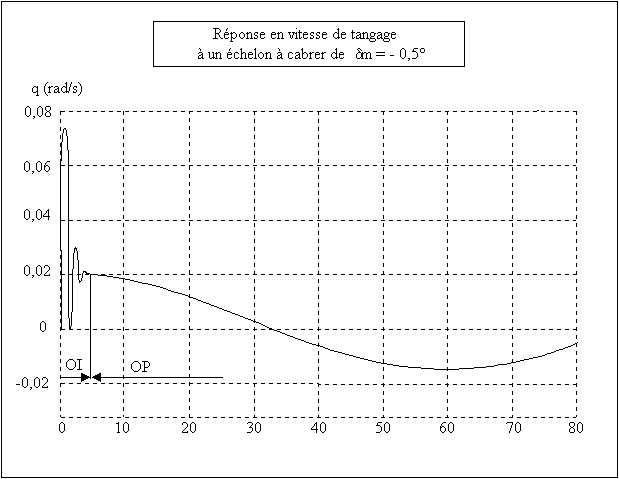
Si l'on enregistre la réponse de la vitesse de tangage à un échelon de profondeur à cabrer, on obtient la courbe ci-après qui montre bien que , ce qui confirme encore la validité des hypothèses de découplage émises.