4-3 Effets transitoires :

L'étude du mouvement longitudinal des avions montre que, à la suite d'une perturbation, ils répondent par deux mouvements généralement bien séparés: l'oscillation d'incidence et l'oscillation phugoïde (dans les cas de centrage généralement rencontrés). De plus, on constate que l'oscillation d'incidence est un phénomène bien plus rapide que l'oscillation phugoïde, ce qui va nous permettre d'étudier successivement ces deux mouvements.

a - Oscillation d'incidence :

Ce phénomène se déroule comme suit:

Un écart d'incidence (provoqué par exemple par une variation de ), en un point de vol équilibré, entraîne l'apparition d'un écart de portance appliqué au foyer F: .

Ceci provoque:

- une rotation de l'avion autour de G, due au moment (à court terme)

- un mouvement vertical du centre de gravité (à long terme),

Cette rotation dépend du signe de :

- G en avant de F : <0 , la rotation tend à diminuer ; il y a rappel en incidence.

- G en arrière de F: >0 , la rotation tend à augmenter ; il y a divergence en incidence.

Dans le premier cas, on a un mode oscillatoire amorti et les écarts en vitesse et en altitude (donc en pente) sont suffisamment faibles pour qu'ils n'affectent pas les forces extérieures. Dans ce mouvement relativement rapide (0,5 à 2 sec), la vitesse et la pente restent pratiquement constantes.

Cependant, ce type de mouvement se caractérise par une pulsation assez élevée et un amortissement relativement faible. Cette combinaison peut présenter un danger pour le pilote; en effet, celui-ci désirant corriger les variations d'incidence le fera avec du retard. L'ensemble avion-pilote peut alors entrer en résonance (phénomène du pompage piloté). Pour éviter ce danger, il convient d'augmenter l'amortissement de ce mode, soit aérodynamiquement (Cmq), soit artificiellement et de façon automatique (stabilisateur ou amortisseur de tangage).

Puisqu'on peut considérer que la pente et la vitesse sont constantes dans ce mouvement, on peut écrire:

puisqu'il s'agit d'écarts par rapport à l'équilibre.

Le modèle complet se réduit donc à:

En prenant la transformée de Laplace de ces équations, il vient:

d'où l'équation caractéristique du mode:

Les racines de l'équation caractéristique sont complexes conjuguées à partie réelle négative. En identifiant cette équation à celle d'un second ordre on en déduit les caractéristiques du mode oscillation d'incidence (indicées OI):

Le temps de réponse TR dépend de x.

On remarque que x est fonction de za et de mq et comme:

et

pour améliorer l'amortissement, il faut modifier Cza (qui dépend de la forme de l'aile) et Cmq (qui dépend de la surface de l'empennage). En travaillant uniquement sur ces deux coefficients, il est donc très difficile de modifier l'amortissement xOI car il faudrait modifier la structure de l'avion.

b - Oscillation phugoïde :

En reprenant la description faite précédemment, on a vu qu'une variation de entraînait un mouvement rapide en rotation autour du centre de gravité de l'avion. La variation en incidence s'amortit pour atteindre une nouvelle position d'équilibre . Cette nouvelle incidence provoque une variation de portance (que l'on suppose >0) appliquée au centre de gravité de l'avion. La modification de l'équilibre des forces entraîne donc les trois phénomènes suivants:

- L'avion va s'élever (>0),

- La traînée de l'avion va augmenter (car augmentation de la portance),

- La composante du poids sur xa (-mg sing), appelée poids-pente, augmente.

En conséquence, la vitesse de l'avion va diminuer, provoquant une diminution de la portance. devient nul, puis négatif, l'avion redescend, donc V augmente...

Ce mouvement est un échange entre l'énergie cinétique et l'énergie potentielle de l'avion à incidence quasiment constante. La variation de V, Z et g est pseudo-sinusoïdale avec le temps. Ce mouvement, l'oscillation phugoïde, est un mouvement pseudo-périodique, très lent, généralement amorti, qui ne présente aucun danger pour le pilote (la lenteur de l'évolution du phénomène fait que le pilote n'a aucun problème pour le contrer).

L'oscillation phugoïde peut aussi être déclenchée par une variation de vitesse >0 (dûe par exemple à >0). Si la poussée, comme nous en avons fait l'hypothèse, a un moment nul en G, un écart crée des forces toutes appliquées en G. Dans ce cas, aucun moment de tangage, ni vitesse de tangage n'apparaissent (en réalité, a et q subissent de très légères variations dont nous ne tiendrons pas compte).

Si on suppose donc que l'avion subit une variation de vitesse >0, ceci provoque une variation de portance appliquée au centre de gravité de l'avion >0. L'équilibre des forces est rompu, et l'avion va s'élever puisque . Simultanément, la pente devient positive, la traînée (>0) et le poids pente (-mg sing) augmentent; ceci entraîne une décélération, donc une diminution de la vitesse.

devient nulle puis négative. L'avion redescend et l'on retrouve le phénomène d'échange d'énergie cinétique et d'énergie potentielle décrit précédemment.

Puisqu'on peut considérer que l'incidence est constante dans ce mouvement, on peut écrire:

puisqu'il s'agit d'écarts par rapport à l'équilibre.

Le modèle complet se réduit donc à:

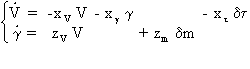
En prenant la transformée de Laplace de ces équations, il vient:

d'où l'équation caractéristique du mode:

Les racines de l'équation caractéristique sont complexes conjuguées à partie réelle négative. En identifiant cette équation à celle d'un second ordre on en déduit les caractéristiques du mode oscillation phugoïde (indicées OP):

Le temps de réponse TR dépend de x.