3-3 Linéarisation des équations :
Afin de pouvoir étudier plus facilement les caractéristiques du modèle longitudinal de l'avion, il faut travailler sur un modèle mathématique simple. La linéarisation des équations du mouvement autour d'un point de vol équilibré en régime permanent (le palier stabilisé en général) permet de l'obtenir.
a - Principe de linéarisation :
Chaque équation du modèle peut s'écrire sous la forme:
dm braquage de la gouverne de profondeur
dt commande des propulseurs
Cette relation est vraie en chaque point de vol, et pour chacune des équations, on effectue un développement en série de Taylor que l'on arrête au premier ordre:
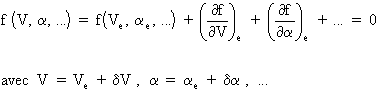
Ce qui revient à écrire que la différentielle totale de f
est nulle. La notation 
signifie qu'après calcul de la dérivée partielle
de f par rapport à x, on donne à tous les paramètres leur
valeur d'équilibre.
Le domaine de validité des équations linéarisées est relativement restreint; on considérera donc que, dans ce domaine, l'atmosphère est isotrope, c'est à dire que:
Pour soulager les écritures, on notera enfin: 
b - Linéarisation des coefficients aérodynamiques :
Coefficient de portance:
Le coefficient de portance peut se linéariser de la façon suivante (on suppose Cz indépendant de
et q):
Coefficient de traînée:
Le coefficient de traînée peut se linéariser de la façon suivante (on suppose Cx indépendant de
Coefficient de moment de tangage:
c - Linéarisation de la poussée :
En supposant que la poussée F ne dépend que de la position
de la manette des gaz (dt) et de la
vitesse (donc indépendante de a, 
et q), on obtient la
relation:
d - Linéarisation des équations du modèle :
La linéarisation des équations demande un développement mathématique long et fastidieux. Les calculs ont donc été repoussés en annexe 4. Cependant, il convient de s'y reporter pour comprendre le changement de notation qui permet de soulager les écritures. Dans les équations linéarisées suivantes, les changements de notations sont:
|
|
|
|
|
|
|
|
Les nouvelles notations représentent les petites variations autour de la valeur d'équilibre.
| ATTENTION : La même notation représentera soit la grandeur réelle, soit les petites variations par rapport à la valeur d'équilibre. Il convient donc, lorsqu'on écrit ou qu'on utilise une équation, de bien savoir à quelles grandeurs on a affaire. |
Pour alléger encore les notations, on remplace dm par m et dt
par t quand ils sont en indice. De
plus, on note 
. On
a alors:
- Equation de propulsion linéarisée:
|
avec:
- Equation de sustentation linéarisée:
|
avec:
- Equation de moment linéarisée:
|
avec:
Sur certains avions, mt peut ne pas être nul (réacteurs sous pylône).
- Equations cinématiques linéarisées:
Dans le modèle avion que l'on cherche, q n'est pas retenu comme variable. On la remplace par a en utilisant la relation:
d'où
|
Pour la dernière équation du modèle on a:
Donc, en tenant compte du changement de notation:
|
