ANNEXE 9

Influence de la tenue d'altitude amortie par l'assiette sur la phugoïde

Le but de cette annexe est de montrer sur un exemple numérique que l'oscillation phugoïde est stabilisée lorsque l'on équipe l'avion d'une tenue d'altitude amortie par l'assiette.

1 Rappels des données :

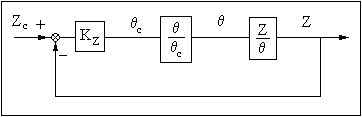
Le synoptique de la tenue d'altitude amortie par l'assiette:

La fonction de transfert liant Z et q a été établie au chapitre 4 en faisant l'hypothèse que l'avion était équipé d'une automanette.

Nous allons montrer que dans le cadre strict de la tenue d'altitude, ce dispositif n'est pas nécessaire.

2 Fonctions de transfert :

La fonction de transfert que l'on peut mettre sous la forme:

Et, la dernière équation du modèle longitudinal donne:

Sachant que pour la tenue d'altitude seul le mode lent (l'oscillation phugoïde) de l'avion naturel nous intéresse, on peut donc considérer que q = 0 dans le modèle avion. Enfin considérant que la tenue d'assiette est concernée par le mode rapide de l'avion, on peut donc écrire pour l'étude du mode lent que q = qc.

Les équations du système concernant se mode sont donc puisque q=a+g:

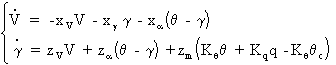
D'après les hypothèses, le terme en zm s'annule, et la transformée de Laplace des équations s'écrit alors:

On peut donc calculer la fonction de transfert liant q et V:

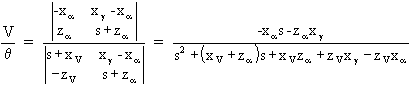
Si l'on reprend les données numériques du point de vol déjà utilisé (chapitre 2) rappelées ci-dessous:

On obtient pour la fonction de transfert:

Les deux pôles de cette fonction de transfert étant réels négatifs, la vitesse de l'avion n'oscille pas et elle est stable (au sens de l'automatique).

De plus, si l'on décompose en éléments simple l'expression précédente, on a:

Le gain statique de chacun des éléments est respectivement:

Le pôle s = -0.094 est donc dominant, le temps de réponse du système sera alors:

Ce mode est donc "relativement" lent, mais si on le compare au temps de réponse de l'oscillation phugoïde (de l'ordre de 6 mn en ce point de vol), on peut donc dire que la phugoïde est stabilisée et que la vitesse peut être considéré comme constante.

Dans l'étude de la tenue d'altitude amortie par l'assiette, cela revient donc à annuler dans les équations du modèle le paramètre vitesse. On retrouve donc les mêmes équations que celles utilisées dans le paragraphe 3 du chapitre 4.

Il faut cependant bien noter que ce raisonnement ne serait plus du tout valable s'il fallait étudier une loi de capture ou de changement d'altitude, ou si dans le cas de la tenue d'altitude amortie par l'assiette, un écart trop important survenait entre l'altitude consigne et l'altitude réelle de l'avion. Sous ces contraintes, pour conserver la validité du modèle utilisé, il faut qu'obligatoirement l'avion soit équipé d'une automanette.