ANNEXE 8

Lieu d'Evans de l'amortisseur de tangage

Le but de cette annexe est de montrer que le lieu d'Evans de l'amortisseur de tangage est, pour les valeurs de Kq donnant des pôles à partie imaginaire non nulle, un arc de cercle centré sur le zéro de .

1- Rappel des données :

Le lieu d'Evans est le lieu des pôles de la fonction de transfert en boucle fermée du système étudié; dans notre cas on a :

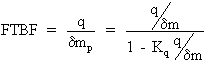
Les points du plan complexe faisant partie de ce lieu vérifient donc l'équation:

La relation liant q et dm étant:

que l'on peut noter:

L'équation à résoudre est donc:

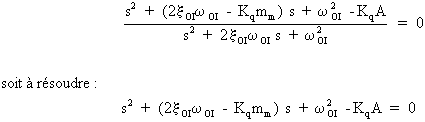
2- Calcul de l'équation du lieu :

Les pôles concernés par cette étude ont une partie imaginaire non nulle, on s'intéresse donc dans la résolution de l'équation ci-dessus au cas du discréminant négatif ().

Dans ce cas, les racines sont complexes conjuguées et s'écrivent:

que l'on peut noter:

avec:

Dire que cette partie du lieu est un arc de cercle centré sur le zéro z0 de implique que a et b vérifient l'équation:

puisque z0 est réel.

Comme z0 = on a:

En effectuant la somme de ces deux termes, on obtient:

Le second membre de l'égalité est bien une constante puisqu'il est indépendant de Kq. De plus, il est positif puisque A > 0 et mm < 0.

Cette partie du lieu d'Evans est donc bien un arc de cercle.