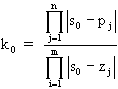
ANNEXE 7

Construction du lieu d'Evans

Le but de cette annexe est de rappeler les règles de construction du lieu des racines (ou lieu d'Evans) d'un système bouclé réglable. Ces différents règles sont énoncées et non démontrées.

1- Système étudié :

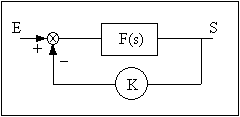
Le système à étudier est le suivant:

La fonction de transfert en boucle fermée du système s'écrit donc:

Trouver les pôles du système, c'est à dire les racines du dénominateur de la fonction de transfert, c'est résoudre l'équation:

Et si l'on veut connaître l'ensemble des solutions possibles, il faut résoudre cette équation pour chaque valeur que peut prendre K (c'est à dire de 0 à l'¥ )!!!

Le lieu d'Evans permet (lorsqu'il est tracé avec précision) de "visualiser" l'ensemble de ces solutions puisqu'il représente le pointage dans le plan complexe des pôles pour toutes les valeurs de K.

Ce lieu est toujours symétrique par rapport à l'axe réel.

2- Règles de construction du lieu :

 Normalisation du gain:

Il s'agit de "normer" les coefficients des termes de plus haut degré au numérateur et au dénominateur de F(s) en posant:

avec dans notre cas d'étude:

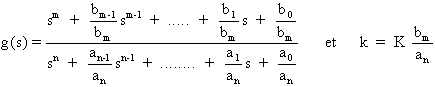
‚ Points de départ du lieu:

Les points de départ du lieu sont les solutions de l'équation pour k=0. Ce sont donc les pôles de g(s) donc de F(s) (c'est à dire les racines du dénominateur de g(s) ou F(s)).

ƒ Points d'arrivée du lieu:

Les points d'arrivée du lieu sont les solutions de l'équation pour . Ce sont donc les zéros de g(s) donc de F(s) (c'est à dire les racines du numérateur de g(s) ou F(s)).

„ Nombre de branches du lieu:

Le nombre de branches du lieu est égal à n.

… Directions asymptotiques du lieu:

Les directions asymptotiques (définies par l'angle noté entre l'asymptote et l'axe réel) du lieu sont données par les relations:

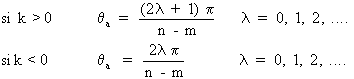
† Points d'intersection des asymptotes avec l'axe réel:

Les points d'intersection des asymptotes avec l'axe réel sont donnés par la relation:

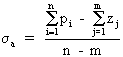
Si l'on note pi les pôles de F(s) ou g(s) (donc les racines du dénominateur de F(s) ou g(s)) et zi les zéros F(s) ou g(s) (donc les racines du numérateur de F(s) ou g(s)). On remarque que est bien un nombre réel.

‡ Points de branchement du lieu:

Les points de branchement du lieu sont donnés par la résolution de l'équation:

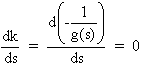
Cela revient à résoudre l'équation:

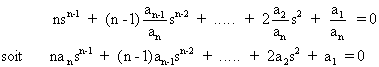
On ne conserve parmi les résultats trouvés que les solutions réelles qui font partie des points de l'axe réel appartenant au lieu (voir ‰ ).

ˆ Relation des arguments:

L' argument en un point du lieu étant l'angle entre l'axe réel et la tangente au lieu en ce point, on montre que, pour chaque valeur de k, si on note zi (i=1,m) les zéros et pj (j=1,n) les pôles de la FTBF, on a la relation:

‰ Points du lieu appartenant à l'axe réel:

Lorsque l'on a positionné dans le plan complexe les points de départ et d'arrivée du lieu, on détermine quels sont les points de l'axe réel qui appartiennent à ce lieu en appliquant les règles énoncées ci-après:

Si k > 0, un point M de l'axe réel appartient au lieu si le nombre total de pôles et de zéros situés à sa droite est impair.

Si k < 0, un point M de l'axe réel appartient au lieu si le nombre total de pôles et de zéros situés à sa droite est pair.

Nota: le nombre 0 est considéré comme pair dans l'application de cette règle.

Une fois effectué l'ensemble de ces calcul, le lieu, ou du moins son allure, peut être tracé. Il permet, par son exploitation d'obtenir un nombre important de renseignements (même qualitatifs) sur les pôles de la fonction de transfert en boucle fermée du système étudié (stabilité, rapidité, factorisation, .....).

Relations complémentaires :

Angle de départ du lieu (en un pôle de g(s))

En notant: ai l'ordre de multiplicité du point d'arrivée (zéro de g(s)) zi

bj l'ordre de multiplicité du point départ (pôle de g(s)) pj

L'angle de départ du lieu au xième point de départ pj=x est:

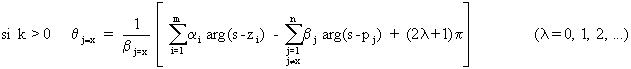
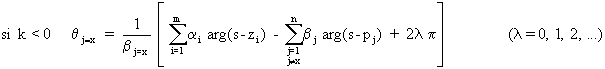
Angle d'arrivée du lieu (en un zéro de g(s)):

Avec les mêmes notation que précédemment, on a la relation:

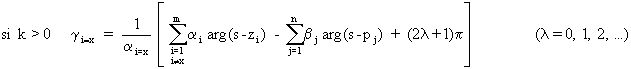
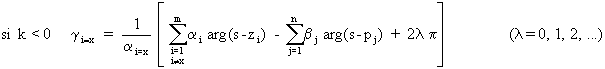
Graduation du lieu en valeurs de k:

Si s0 est un point du lieu, la valeur de k notée k0 qui lui correspond est donné par la relation: