ANNEXE 6
Représentation d'état - Rappels
Le but de cette annexe est de rappeler la notion et les principales propriétés de la représentation d'état des systèmes linéaires continus. Elle ne se substitue donc pas au cours d'automatique sur cette théorie et est volontairement restreinte aux résultats directement liés à l'étude du pilote automatique.
1- Notion d'état :
"L'état" d'un système est le nombre minimum de variables nécessaires (notée généralement x1, x2, ...., xn) pour le définir et en connaître l'évolution à partir de tout instant t0 lorsqu'on en connaît la commande.
L'état d'un système est "la mémoire minimale" nécessaire pour déterminer le futur.
2- Représentation d'état :
La représentation d'état est une notation matricielle, reliant, à partir des équations différentielles régissant le système étudié, l'état du système, sa commande et son ou ses paramètres de sortie (grandeur que l'on veut étudier).
La notation généralement adoptée pour cette représentation d'état est la suivante:
avec pour un système à n états:
X le vecteur d'états [n x 1]
U le vecteur de commande [m x 1]
Y le vecteur de sortie [q x 1]
A la matrice d'état ou dynamique [n x n]
B la matrice d'entrée ou de commande [n x m]
C la matrice de sortie [q x n]
D la matrice de transfert direct [q x m]
Dans le cadre de ce cours, l'ensemble des études concernent des systèmes mono-entrée, mono-sortie et il n'y a pas de couplage entrées-sorties. Les dimensions des vecteurs ou matrice sont donc:
X le vecteur d'états [n x 1]
U le vecteur de commande [1 x 1]
Y le vecteur de sorties [1 x 1]
A la matrice d'état ou dynamique [n x n]
B la matrice d'entrée ou de commande [n x 1]
C la matrice de sortie [1 x n]
D la matrice de couplage entrées-sorties D = 0
La représentation schématique du système est donnée par:
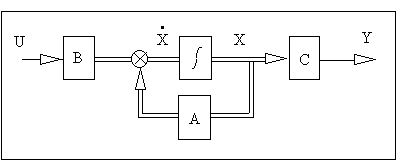
3- Propriétés :
a- Généralités
La modélisation d'un système peut se faire par une fonction de transfert ou par une représentation d'état. Ces deux représentations sont équivalentes.
Il faut noter cependant que si la fonction de transfert est unique, pour un même système, la représentation d'état est multiple. En effet, la formulation matricielle de la représentation d'état sous entend que l'étude du système s'effectue dans une base (au sens mathématique du terme). Ainsi, pour tout couple de matrice M, M-1 (représentatif d'un changement de base) on montre qu'en posant
on obtient la nouvelle représentation (strictement équivalente)
 |
avec |  |
b- Equation caractéristique :
Si pour un système on a:
fonction de transfert
L'équation caractéristique de ce système est:
|
Les racines de cette équation sont les modes du système.
c- Forme canonique de la représentation d'état:
Il existe trois formes canoniques de la représentation d'état. Dans ce cours une seule est utilisée: La représentation d'état sous forme "compagne horizontale".
Si l'équation caractéristique du système étudié est:
la forme compagne horizontale est:
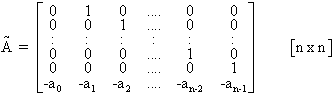
pour laquelle on peut toujours choisir
La notation ~ est réservée dans ce polycopié à l'écriture des matrices en base compagne horizontale. Cette représentation est la plus adaptée à la commande et à la correction par retour d'état.
Pour une représentation d'état (A, B, C) donnée sous une
forme quelconque, on trouve la matrice M permettant de passer
dans la base compagne horizontale (
) par les calculs suivants:
si on note 
mi
est de dimension [n x 1]
on a: 
Le calcul de M-1 s'effectue après avoir trouvé M (M-1 existe si (A, B, C) est gouvernable).
Les relations entre bases sont alors:
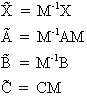
Si l'on note 
,
on a le résultat remarquable pour la fonction de transfert:
4- Fonction de transfert (FT) - Représentation d'état (RE) :
RE è FT :
Si H(s) est la fonction de transfert du système étudié reliant la sortie y à l'entrée u on a:
Dans le cas particulier du modèle avion obtenu dans ce cours, les composantes du vecteur d'état sont les paramètres d'étude de l'avion (V la vitesse, g la pente, a l'incidence, q la vitesse de tangage, Z l'altitude). La commande étant dm, pour trouver, à partir de la représentation d'état, la fonction de transfert entre dm et l'un des paramètres considéré comme la sortie du système, il faudra pour appliquer la formule ci-dessus prendre la matrice C telle que:
FT è RE :
Si H(s) s'écrit d'une façon générale:
on obtient directement la représentation d'état sous forme compagne horizontale en écrivant:
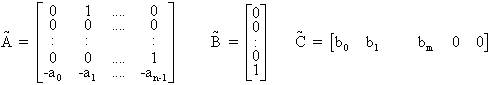
Il est très important de noter que cette méthode systématique ne peut s'appliquer que si le coefficient du terme de plus haut degré en s du dénominateur de la fonction de transfert a été normalisé à 1.
