ANNEXE 5
Amortisseur de tangage
Le but de cette annexe est d'expliquer de la façon la plus "pratique" possible le concept et l'efficacité d'un amortisseur de tangage. On ne rencontrera donc pas dans ce qui suit de démonstration mathématique, mais plutôt une approche physique de la correction nécessaire à apporter à l'avion. Ces explications sont donc basées sur "l'expérience vécue" des réactions d'un avion à la commande de profondeur.
Pour conserver le lien avec le cours, on rappelle que:
- la commande de profondeur représentative du braquage de la gouverne de l'empennage horizontal, est notée dm.
- dm < 0 correspond à un ordre à cabrer.
A un échelon à cabrer dm1 la réponse en incidence de l'avion est donnée par la courbe .
Le pilote "tire" sur le manche: après stabilisation, l'incidence a augmenté. Le danger décrit dans le cours vient des oscillations précédant cette stabilisation.
Améliorer l'amortissement revient à diminuer l'amplitude et
le nombre des oscillations. Si on applique un échelon à cabrer dm2 tel que 
à ce système, on
obtient la réponse ‚ .
L'amplitude du premier pic A1 est moins importante, mais les oscillations sont bien sûr toujours présentes et la valeur finale de l'incidence n'est plus celle que l'on désirait pour une commande dm1 (Vf1>Vf2).
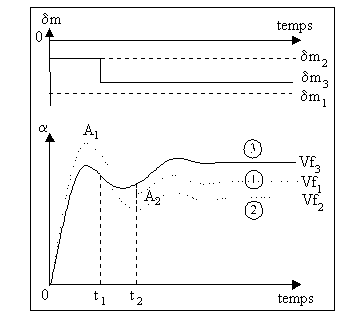
En revanche, si à partir de l'instant t1
on modifie dm2
en dm3 telle que
, l'amplitude du
deuxième pic A2 va être augmentée, et,
entre les instants t=0 et t=t2, on pourra
considérer que l'amortissement du système est amélioré.
Cependant, au-delà de l'instant t2, le
système va évoluer selon son comportement naturel, donc
osciller et atteindre une valeur finale Vf3
différente de Vf1.
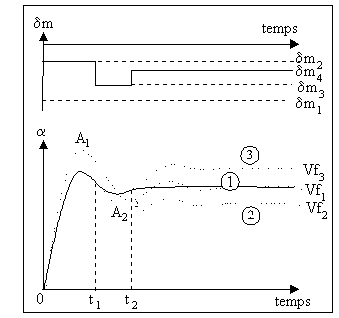
Il faut donc de nouveau modifier la commande, et à partir de
l'instant t2 appliquer dm4 telle que 
. En réitérant ce processus jusqu'à stabilisation
à la valeur finale désirée, on montre que l'on peut, grâce à
la commande, améliorer l'amortissement du système.
De façon naturelle, c'est ce qu'essaierait de faire le pilote aux commandes d'un avion présentant de telles oscillations. Malheureusement, si ces oscillations sont trop rapides, le pilote ne fera que les amplifier en provoquant le phénomène de pompage piloté.
Ainsi, bien que le pilote commande au manche un braquage dm1, c'est la séquence dm4 qui doit effectivement parvenir en entrée du processus. Il faut donc pour améliorer la dynamique du système superposer aux ordres du pilote des variations de braquage afin d'obtenir ce profil de commande. Cependant, reproduire une telle séquence n'est pas possible directement car:
- La commande n'est pas continue (donc physiquement irréalisable)
- Rien ne permet de connaître les instants t1 et t2 ou les amplitudes de dmi de la commande modifiée.
Cependant, la synthèse de cette étude qualitative permet d'apporter la conclusion suivante:
l'ordre envoyé étant dans notre exemple négatif (ordre à cabrer), il faut ajouter entre les instant t=0 et t=t1 une grandeur positive à dm1 pour obtenir dm2 puis entre les instants t=t1 et t=t2 une grandeur positive à dm2 pour obtenir dm3, ainsi de suite jusqu'à stabilisation. Si l'on regarde la variation de la vitesse de tangage, on voit sur le schéma qui suit qu'à un coefficient d'adaptation près, elle évolue dans le sens qui nous intéresse.
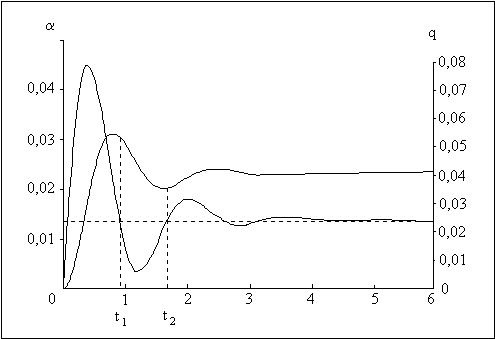
Donc, en superposant aux ordres du pilote un ordre de braquage de la gouverne proportionnel à la vitesse de tangage, on réussit à diminuer, de façon automatique et systématique, les oscillations de l'incidence de l'avion.