ANNEXE 4
Linéarisation de l'équation de propulsion
Il est rappelé, pour ce développement, que l'on suppose r = re = cste et que les coefficients et la poussée sont indépendants de l'altitude.
La linéarisation de l'équation de propulsion s'obtient en effectuant le développement de Taylor au premier ordre autour du point de vol équilibré, ce qui revient à écrire que la différentielle totale de l'équation est nulle. On a:
![]()
![]()
ü
é
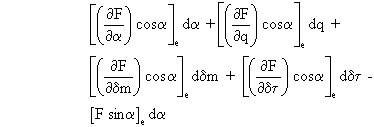
ā
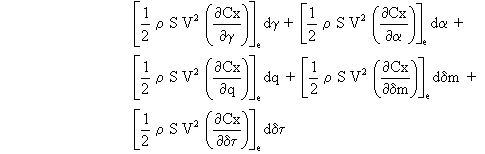
ä
En regroupant les termes, il vient:
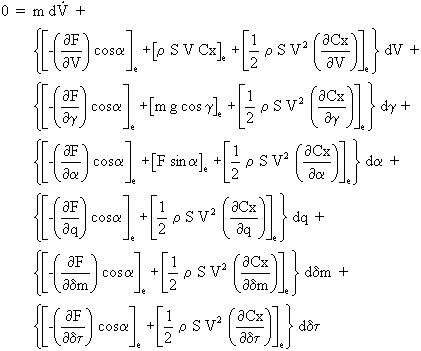
Si on suppose que la poussée F est indépendante de a, q, g, dm et que le coefficient de traînée Cx est indépendant de q, g et dt on a si l'on note ![]() :
:
Fa = Fq = Fg = Fdm = Cxq = Cxdt = Cxg = 0
La relation devient alors:
![]()
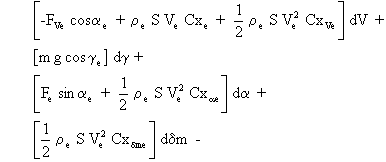
![]()
En divisant, pour des raisons d'homogénéité, l'équation par Ve et en posant ![]() on obtient:
on obtient:
![]()
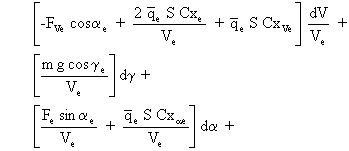
![]()
![]()
Limiter le développement de Taylor au premier ordre implique que cette relation n'est valable que pour les petits mouvements autour du point de vol équilibré. On peut donc remplacer les différentielles par les écarts notés D.
![]()
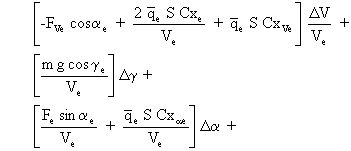
![]()
![]()
Afin de simplifier les notations, on effectue les changements de variable suivants:
|
|
|
|
|
|
|
|
|
|
Il est donc très important de retenir que la même notation représentera soit la grandeur réelle, soit les petites variations par rapport à la valeur d'équilibre.
L'équation de propulsion linéarisée s'écrit alors:
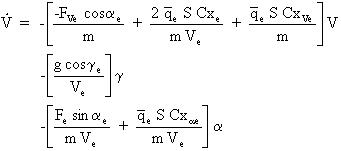
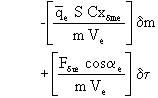
que l'on met sous la forme:
|
|
Linéarisation de l'équation de sustentation
Avec les mêmes hypothèses que précédemment, la linéarisation de l'équation de sustentation s'obtient en effectuant le développement de Taylor au premier ordre autour du point de vol équilibré, ce qui revient à écrire que la différentielle totale de l'équation est nulle. On a:
![]()
![]()
ü
é
![]()
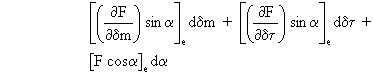
ā
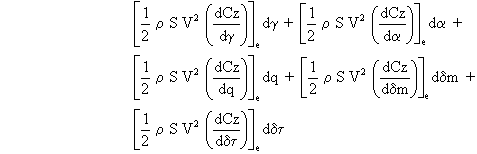
ä
En adoptant les notations des dérivées partielles données pour l'équation de propulsion et en remarquant que:
![]() (la pente est constante en un point de vol équilibré)
(la pente est constante en un point de vol équilibré)
La poussée F est indépendante de g, a, q et dm (donc Fa = Fq = Fg = Fdm = 0)
Le coefficient de portance Cz est indépendant de g, q et dt (donc Czq = Czdt = Czg = 0)
La relation devient alors:
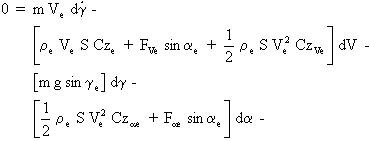
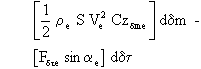
En divisant par mVe et en passant des différentielles aux écarts, on obtient:
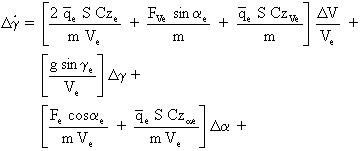
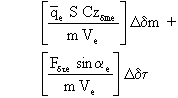
En adoptant le changement de notations utilisé dans la linéarisation de l'équation de propulsion, il vient:
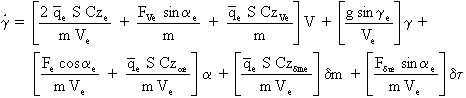
que l'on met sous la forme:
|
|
Linéarisation de l'équation de moment
Avec les mêmes hypothèses que précédemment, la linéarisation de l'équation de moment s'obtient en effectuant le développement de Taylor au premier ordre autour du point de vol équilibré, ce qui revient à écrire que la différentielle totale de l'équation est nulle. On a:
![]()
![]()
ü
é
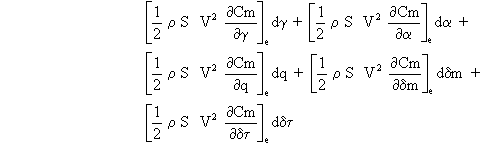
En adoptant les notations des dérivées partielles données pour l'équation de propulsion et en remarquant que:
Le coefficient de moment Cm est indépendant de g et dt (donc Czdt = Czg = 0)
![]() (voir paragraphe 3-3-b Linéarisation des coefficients aérodynamiques)
(voir paragraphe 3-3-b Linéarisation des coefficients aérodynamiques)
La relation devient alors:

En divisant par B et en passant des différentielles aux écarts, on obtient en notant que Cme=0:
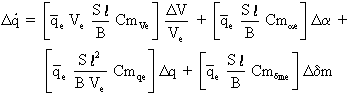
En adoptant le changement de notations utilisé dans la linéarisation de l'équation de propulsion, il vient:
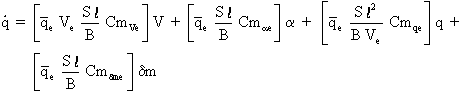
que l'on met sous la forme:
|
|