ANNEXE 3

Séparation des mouvements

L'étude du mouvement des avions montre qu'il existe un mouvement longitudinal pur. Le but de cette annexe est de déterminer quelles équations du modèle complet le régissent.

Un mouvement longitudinal pur ne doit intéresser que les variables u, w, q, q et ZG.

L'examen du modèle complet trouvé en annexe 2 montre que l'on a deux groupes d'équations:

1- Groupe d'équations longitudinales :

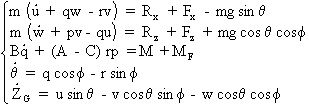
Concernant les dérivées des paramètres en u, w, q, q et ZG.

2- Groupe d'équations transversales :

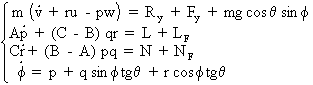
Concernant les dérivées des paramètres en v, p, r et f.

3- Conditions d'existence du mouvement longitudinal pur :

Ce mouvement n'intéresse que les variables u, w, q, q et ZG. Il faut que les variables v, p, r et f soient constantes. Les équations du mouvement transversal doivent être vérifiées quels que soient u, w, q, q et ZG.

Donc, si l'on indice 0 pour désigner la valeur constante des variables, il vient pour le groupe d'équations transversales:

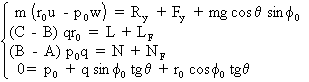
Ce système ne peut être satisfait que s'il est indépendant des variables longitudinales. Il faut donc que:

Le groupe d'équations transversales se réduit donc à:

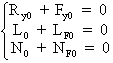
Pour avoir quels que soient u, w, q, q et ZG il faut que les plans Gxa za et Gx z soient confondus. Pour cela, il faut que le dérapage b = 0.

On a alors:

Par conséquent:

On doit donc avoir une configuration symétrique des propulseurs.

4- Caractéristiques du mouvement longitudinal pur :

- Les plans Gxa za et Gx z sont confondus

- Les ailes sont horizontales f = 0

- Le dérapage est nul b = 0

- Les propulseurs ont une configuration symétrique et les termes gyroscopiques dus aux parties tournantes sont négligeables