ANNEXE 2

Equations de la mécanique

Dans cette annexe sont établis les systèmes d'équations qui régissent le mouvement de l'avion. Les calculs étant effectués dans le repère avion, on rappelle tout d'abord l'ensemble des paramètres et leurs notations dans ce repère.

1- Rappel des notations

a- Coordonnées :

Positionnement du centre de gravité de l'avion par rapport à la terre.

Ces coordonnées sont notées: XG, YG, ZG.

b- Positions angulaires :

Angles reliants le repère avion au repère terrestre (angles d'Euler).

Ces angles sont notés: y, q, f.

c- Vitesse linéaire :

Vitesse de l'avion par rapport à la masse d'air environnante.

Le vecteur vitesse est noté . Ses composantes sont notées:

d- Vitesse angulaire :

Vecteur vitesse instantanée de rotation de l'avion par rapport aux axes fixes X0, Y0, Z0.

Il est noté . Ses composantes sont notées:

e- Tenseur d'inertie :

Il est noté et est supposé constant.

Le système est entièrement défini par ces douze variables. Il faut alors trouver douze équations si l'on veut obtenir le modèle complet de l'avion afin de caractériser le comportement de ses évolutions.

f- Forces aérodynamiques :

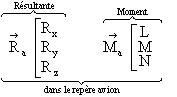
g- Forces de propulsion :

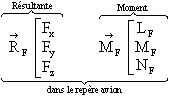
h- Force de pesanteur :

Le poids est la seule force de masse considérée. Elle est verticale, dirigée vers le bas et son moment en G est nul.

Dans le repère avion, ses composantes sont:

2- Systèmes d'équations :

a- Equations de forces :

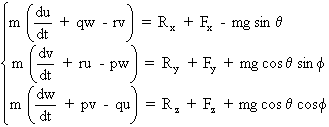
b- Equations de moments :

Si on considère que les axes avions sont confondus avec les axes principaux d'inertie donc E = 0, ces relations s'écrivent:

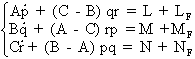
c- Relations cinématiques :

Ces relations lient les vitesses angulaires et les angles.

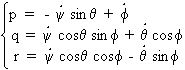
Les relations inverses donnent:

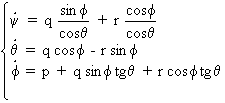
d- Equations de la trajectoire :

Dans le repère avion, les équations de la trajectoire s'écrivent:

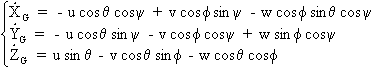
On a donc un système de douze équations à douze inconnues: (u, v, w), (p, q, r), (y, q, f), (XG, YG, ZG).

On remarque de plus que XG, YG et y peuvent être déterminés dès lors que l'on connaît les autres variables, et n'interviennent pas dans leurs expressions.

Le système à étudier est donc régi par les neuf équations suivantes: