![]() Obtention d'un modèle paramétrique par minimisation de l'erreur de sortie
Obtention d'un modèle paramétrique par minimisation de l'erreur de sortie
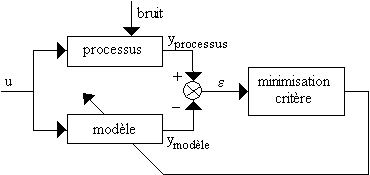
Critère d'identification : minimisation de l'erreur de sortie.
·
Le modèleLa structure est choisie a priori ou, plus généralement, établie par rapport aux équations disponibles (physiques, chimiques, électroniques, ...). La connaissance a priori joue ici un rôle primordial.
·
Le critèreLe critère quadratique à minimiser porte sur l'erreur de sortie : ![]()
·
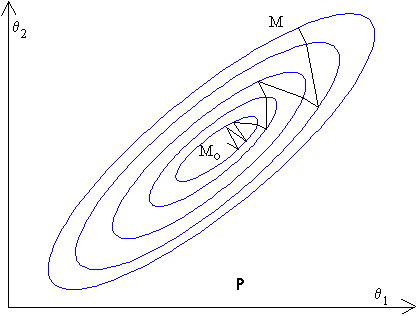
L'espace paramétriqueSi q est de dimension m, on peut associer à ces m paramètres un espace P de dimension m, appelé espace paramétrique.
Un point P Î P est défini par les valeurs des m paramètres.
A chaque point P de P correspond un critère J(M) et un modèle.
·
Etude du critère au voisinage du minimumSoit ![]() le point de P correspondant au minimum du critère et M un point situé dans son voisinage.
le point de P correspondant au minimum du critère et M un point situé dans son voisinage.
Le critère au point M est obtenu par développement de Taylor, arrêté à l'ordre 2 :
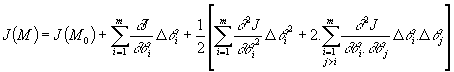
Si l'on pose : 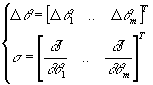 et
et 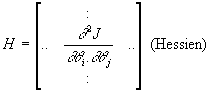
On a : ![]()
·
Méthode directe (d'ordre 0)On utilise uniquement la valeur du critère.
Ä
tabulation :le critère est évalué en différents points de l'espace paramétrique.
Ä
ajustement cyclique des paramètres :- on part d'une estimation initiale. On fixe tous les paramètres sauf un.
- ayant ainsi réduit le problème à une seule dimension, on recherche la valeur du paramètre variable correspondant au critère minimum.
- on fait ensuite de même avec le paramètre suivant.
- après m recherches mono dimensionnelles, on obtient une estimation qm.
- on recommence le cycle à partir de cette nouvelle estimation.
Les performances de cet algorithme ne sont généralement pas satisfaisantes.
·
Méthode du gradient (d'ordre 1)On utilise cette fois le gradient du critère : ![]()
Cette méthode consiste à se déplacer dans la direction inverse de celle du vecteur gradient au point courant (on suit la direction de plus grande pente).
Si i désigne le numéro de l'itération, la mise à jour des paramètres se fait de la manière suivante :
![]() avec
avec ![]()
G
peut être choisi constant, mais sa taille constitue un problème délicat. Généralement, il est ajusté à chaque pas de calcul.Cette méthode peut sembler avoir d'excellentes performances. Cependant, la direction de plus grande pente est une propriété locale qui peut donc nous amener sur un minimum local, situé assez loin du minimum global.
En définitive, la méthode du gradient est moyennement performante. Elle a notamment un mauvais comportement si le critère présente des "vallées longues et étroites" (problème de vitesse de convergence).
·
Méthode du second ordreAu second ordre et autour du point courant, le critère se développe sous la forme :
![]()
Au voisinage du minimum, ![]()
et ![]() soit
soit ![]()
Cette formule constitue la base des algorithmes du second ordre.
En effet, dans ce cas, ![]()
Ce qui conduit à la formulation de Newton-Raphson :
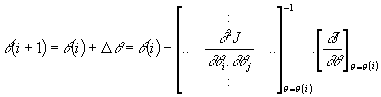
Cet algorithme possède de très bonnes performances au voisinage du minimum.
Son principal inconvénient réside dans la complexité d'évaluation et la nécessité d'inversion du gradient second et dans le coût de calcul associé.
Dans le cas du critère quadratique, on a : ![]()
![]()
![]()
Au voisinage du minimum, ![]() . Si l'on néglige le second terme du gradient second, on aboutit à la formulation de Gauss-Newton :
. Si l'on néglige le second terme du gradient second, on aboutit à la formulation de Gauss-Newton :
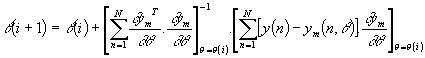
Le principal avantage de cette méthode est que l'on n'a besoin de calculer que des dérivées premières (charge de calcul moins importante), avec des performances proches de celles de l'algorithme de Newton-Raphson au voisinage du minimum.
·
Méthode pratiqueLoin du minimum, les algorithmes du second ordre présentent certaines difficultés. On aura donc intérêt à commencer la minimisation par une méthode de type gradient. Au voisinage du minimum, on pourra basculer sur une méthode du second ordre