Les différentes structures de modèle

 Méthodes paramétriques et non paramétriques

 Les réponses à des signaux définis :

On sait qu'un système linéaire est complètement caractérisé par la connaissance de sa réponse indicielle ou de sa réponse impulsionnelle. En effet, la fonction de transfert d'un système est la transformée de sa réponse impulsionnelle, ou encore la transformée de la dérivée de sa réponse indicielle.

On peut donc identifier un système en déterminant sa réponse impulsionnelle, sa réponse indicielle ou sa réponse fréquentielle. Autrement dit, le système est identifié par une fonction qu'il faut connaître sur un nombre très élevé, voire infini, de valeurs.

On parle alors de description non paramétrique du système.

On utilise alors des méthodes d'identification non paramétrique.

La représentation d'état :

Un système peut être représenté par un modèle d'état :

Pour définir ce système, il suffit donc dans ce cas de connaître un nombre fini de paramètres (les coefficients des matrices).

On parle alors de description paramétrique du système.

On utilise alors des méthodes d'identification paramétrique.

Dans le cas mono-entrée, mono-sortie :

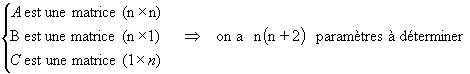
Remarque : on cherchera toujours à identifier le minimum de paramètres.

En particulier, si cela est possible, on choisira une représentation canonique :

exemple :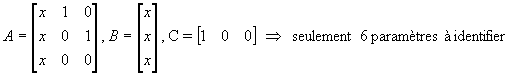

La fonction de transfert :

La fonction de transfert d'un système, définie comme la transformée de sa réponse impulsionnelle, apparaît comme une description non paramétrique du système.

Or, on sait aussi que ; La fonction de transfert s'exprime donc aussi sous forme d'une fraction rationnelle, définie par un nombre fini de paramètres.

La fonction de transfert apparaît donc aussi comme une description paramétrique du système.

exemple :

De manière plus générale, en présence d'un bruit quelconque, on a :

Ce bruit est souvent représenté par le passage d'un bruit blanc à travers une fonction de transfert :

Le nombre de paramètres à identifier augmente donc.

On distingue plusieurs modèles pour représenter un système par fonction de transfert. Les principaux sont présentés ci-dessous :

Ä Le modèle ARX

Un processus auto-régressif (AR) correspond au passage d'un bruit blanc à travers un filtre stable.

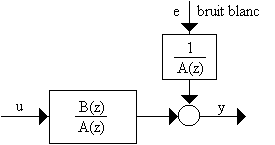
Pour modéliser un système comportant une entrée et soumis à une perturbation, on peut donc utiliser un modèle ARX (X pour entrée externe).

C'est un modèle dit "erreur d'équation" (A(z) est facteur commun).

 

 

Avantages : faible nombre de paramètres à identifier.

Inconvénients : manque de liberté pour décrire les propriétés du terme de perturbation.

 

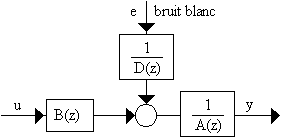
Ä Le modèle ARARX

variante du modèle ARX.

C'est un autre modèle dit "erreur d'équation".

 

 

Avantages : meilleure modélisation, notamment pour le terme de perturbation.

Inconvénients : plus grand nombre de paramètres à identifier.

 

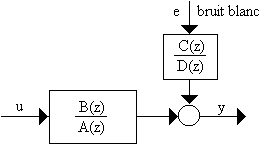
Ä Le modèle ARMAX

Un processus auto-régressif à moyenne ajustée (ARMA) correspond au passage d'un bruit blanc à travers un filtre comportant des pôles et des zéros.

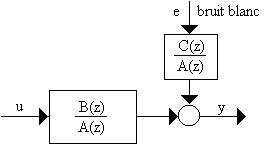
Pour modéliser un système comportant une entrée et soumis à une perturbation, on peut donc utiliser un modèle ARMAX (X pour entrée externe).

C'est encore un autre modèle dit "erreur d'équation".

 

 

Avantages : meilleure modélisation, notamment pour le terme de perturbation.

Inconvénients : plus grand nombre de paramètres à identifier.

 

Ä Le modèle ARMAX avec pôles différents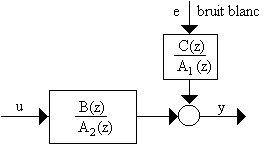

 

Ä Le modèle OE

Modèle dit "erreur de sortie" (Output Error).

 

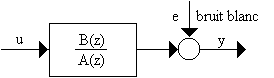
Ä Le modèle de Box-Jenkins

Variante plus riche du modèle OE