Lors des chapitres précédents, les systèmes étudiés admettaient des signaux déterministes i.e. les mêmes causes engendrent les mêmes effets.
- états déterministes
- mesures des états déterministes
A la notion de signaux déterministes, on oppose la notion de signaux aléatoires pour lesquels le hasard intervient. Dans la pratique, les signaux sont bruités et confèrent au système un comportement aléatoire.
- des bruits se superposent aux états, on les appelle bruits díétat.
- les capteurs, leur chaîne díacquisition et de traitement bruitent les mesures, on parle de bruits de mesure.
Le moteur à courant continu de líasservissement de position étudié en première année peut être caractérisé par le vecteur díétat :
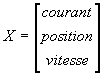
et le vecteur de mesure :
![]()
Bruits díétat
La résistance de líinduit parcourue par le courant díinduit i est à líorigine díun bruit thermique qui se traduit par un courant de bruit lequel síajoute au courant délivré par le générateur.
Líusure des liaisons mécaniques, les frottements secs sont à líorigine de vibrations qui bruitent les états vitesse et position.
Bruits de mesure
Le potentiomètre de recopie est également sujet au bruit thermique.
La chaîne de traitement ( amplificateurs, filtres, etc. ) est alimentée via des régulateurs par le réseau. Les variations de ce dernier affectent les mesures. Les éléments constitutifs de cette chaîne sont réalisés par des semi-conducteurs, ces derniers génèrent du bruit de grenaille.
Lors du chapitre consacré aux observateurs déterministes nous avons montré quíil était possible de reconstruire les états non mesurés et non mesurables díaprès líobservation des sorties et des commandes (sous réserve que le système soit observable). Le problème posé dans ce cours est identique, avec toutefois une difficulté supplémentaire, les états et les mesures sont bruités. Il síagit donc de reconstruire au mieux ces états. On élabore un observateur stochastique ( du grec stokhastikos Ď conjecturalí ).
Le tableau suivant récapitule les stratégies élaborées en matière de commande et díobservation pour un système décrit par sa représentation díétat.
|
Stratégie |
Commande |
Observateurs |
|
Placement de pôles |
Commande modale |
Observateur identité |
|
Minimisation díun critère |
Commande optimale LQ, principe du minimum |
Observateur stochastique : Les états et les mesures sont aléatoires, on minimise un critère statistique |
![]() Exemple de critère statistique
Exemple de critère statistique
Chercher une régression qui minimise la somme quadratique des erreurs.

Figure 1
Les signaux sont aléatoires, par conséquent on níen a quíune connaissance probabiliste.
On considère un vecteur aléatoire x=[x1, x2...xn]T où chaque composante est une variable aléatoire (v.a) pouvant prendre un ensemble continu de valeurs. Dans ce cours, x désigne indifféremment le vecteur díétat, de mesure, bruits díétat et bruits de mesure.
p(x1,x2...xn)
qui vérifie : Prob(x'< x < xí +dx) = p(x).dx1.dx2...dxn![]() líévénement certain.
líévénement certain.
Illustration dans le cas d'un vecteur à 2 composantes dont les densités de probabilités sont gaussiennes.

Figure 2
![]() La valeur moyenne ou espérance mathématique
La valeur moyenne ou espérance mathématique

Le vecteur est dit centré lorsque E[ X ] = 0
S
xx = Var[X] =
S
xx =
S
xx=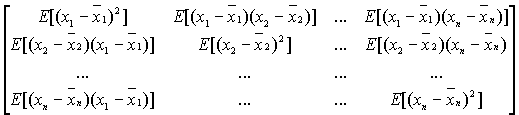
Ā
La matrice de variance est symétrique définie positive.ā
Les termes diagonaux sont les variances des v.a : sii2 =É
La trace de la matrice de variance représente la somme des variances![]()
Ą
Lorsque les composantes non diagonales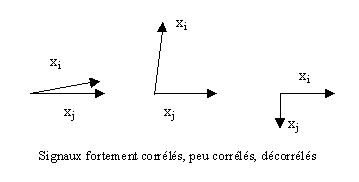
Figure 3
Ö
Lorsque la matrice est diagonale, tous les états sont décorrélés.![]()
La covariance peut porter sur deux vecteurs différents X et Y ou sur un même vecteur considéré à des instants différents [ X(t), X(t + t )].
On modélise les bruits díétat et de mesure par des bruits blancs.
![]() Définition et propriétés
Définition et propriétés
Dans ce cours, on suppose les états et les mesures bruités par des bruits blancs. Le bruit blanc b(t) est défini comme un processus stochastique dont la densité spectrale de puissance reste constante sur une large bande. Par analogie avec la lumière blanche qui est composée de radiations de toutes les longueurs d'ondes.

Figure 4
Sbb(f) représente la distribution fréquentielle de la puissance totale du signal. Lorsque f0 ® • La densité spectrale de puissance ® • . La densité spectrale de puissance est par définition la transformée de Fourier de la fonction díintercorrélation qui est assimilable à la covariance Cbb(t). ( sous réserve que le signal soit à valeur moyenne nulle et en faisant líhypothèse díergodicité ).
Cov[ b(t), b(t + t ) ] = Cbb(t) = F-1{Sbb(f)} = 

Figure 5

Figure 6
Quelle signification donner à Cbb(t) ?
Cbb(t) montre comment la valeur prise par b(t) influence la valeur prise par b(t + t ). En t = 0, la ressemblance de b(t) et b(t + t ) est totale et la fonction Cbb(t) est maximale. Lorsque Cbb(t) síannule, la valeur prise par b(t) níinfluence pas b( t+ t ). Les bruits sont décorrélés.
Dans le cas díun bruit blanc idéal, f0 ® • , Cbb(t) tend vers une impulsion de Dirac : Cbb(t) calculée au sens des distributions vaut k≤.d(t- t ). La variance ® • et les bruits observés à deux instants différents sont décorrélés.
![]() Cas vectoriel
Cas vectoriel
On considère le cas díun vecteur de bruits blancs ( cas des n bruits blancs associés à chaque état ou à chacune des mesures ) :
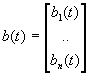
S
bb = Cov[b(t), b(s)] = B(t).d(t-s)S
bb= = B(t).d(t-s)
= B(t).d(t-s)
Dans la suite de ce cours on note :
![]() la moyenne de X
la moyenne de X
 la covariance de líétat
la covariance de líétat
W(t) le bruit díétat, blanc et centré, stationnaire
![]() la covariance du bruit díétat
la covariance du bruit díétat
V(t) le bruit de mesure, blanc et centré, stationnaire
![]() la covariance du bruit de mesure
la covariance du bruit de mesure
![]() les bruits díétat et de mesure sont non-corrélés
les bruits díétat et de mesure sont non-corrélés
![]() les bruits de mesure et les états sont non-corrélés
les bruits de mesure et les états sont non-corrélés
![]() líétat initial et les bruits díétat sont non-corrélés
líétat initial et les bruits díétat sont non-corrélés
Le système est décrit par sa représentation díétat. Les état et les mesures sont bruitées par des bruits blancs. On ne síinteresse pas à la commande qui est déterministe. On se propose pour un tel système de décrire les lois díévolution des deux premiers moments statistiques, líespérance et la variance.

Figure 7
Un tel système, excité par des bruits díétat et de mesure est appelé processus stochastique. Il est composé :
![]() Un processus stochastique de mesure
Un processus stochastique de mesure
Y = C.X + V
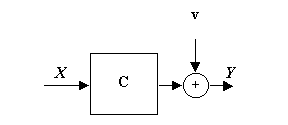
Figure 8
Evolution de líespérance
:Evolution de la covariance
:
Un processus stochastique Markovien peut être décrit comme líétat díun système excité par un bruit blanc. Il est équivalent de montrer quíun processus Markovien est díun point de vue stochastique un processus à mémoire minimale i.e.
![]()
Pour un processus gaussien dont la densité de probabilité est complètement caractérisée par sa moyenne et sa variance, cela revient à écrire que líévolution future (t > u) de ces moments statistiques est conditionnée par E[x(u)] et Var(x(u)). Le passé i.e. la connaisance de E[x(t1)], Var(x(t1)) níenrichit pas la connaissance des phénomènes étudiés.

Figure 9
Avant díétablir les propriétés díun tel processus, on rappelle les résultats relatifs à la résolution de líéquation díétat,
![]()
y
est la matrice de transition dont les propriétés sont rappelées en annexe (3), (4), (5)."
q < t0, X(q) níapporte aucune information quant à líévolution de la trajectoire díétat. Toute líinformation est contenue dans X(t0). Cíest un cas de figure analogue à celui des processus Markoviens.Díaprès la figure précédente, on a :
![]()
![]()
Evolution de líespérance
:![]()
|
|
En dérivant S(t) par rapport au temps et en tenant compte des propriétés de la matrice de transition, il vient :
|
|
Ces deux résultats sont par la suite díun intérêt capital
. Leur démonstration est donnée en annexe.Remarque : Lorsque le bruit d'état agit à travers une matrice B, on a :
![]()
On veut réaliser un observateur linéaire qui reconstruise au mieux les états du système. On rappelle que ces derniers ainsi que les mesures sont bruités. Pour reconstruire le vecteur díétat ![]() on dispose de líensemble des mesures Y jusquíà líinstant t. Un bon estimateur doit annuler líerreur díestimation. Dans le cas díun observateur stochastique, on raisonne sur des considérations probabilistes, il faut que l'erreur díestimation en moyenne soit nulle et que la dispersion de líerreur autour de zéro soit la plus petite possible.
on dispose de líensemble des mesures Y jusquíà líinstant t. Un bon estimateur doit annuler líerreur díestimation. Dans le cas díun observateur stochastique, on raisonne sur des considérations probabilistes, il faut que l'erreur díestimation en moyenne soit nulle et que la dispersion de líerreur autour de zéro soit la plus petite possible.
Ā
la structure de líobservateur stochastique est identique à celle díun observateur déterministe
Figure 10
Equations de líestimateur :
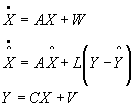
ā
Líobservateur est non biaisé ce qui signifie qu'en moyenne líerreur est nulleEn effet :
![]() qui admet la solution :
qui admet la solution :
![]()
![]()
Le second membre est de moyenne nulle puisque les bruits sont par hypothèse centrés ; le premier terme est nul si les conditions initiales sont parfaitement déterminées, alors e(t0)=0.
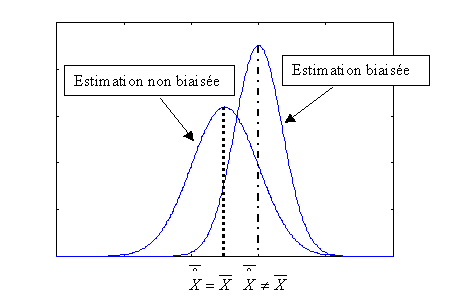
Figure 11
La méconnaissance des conditions initiales, une mauvaise modélisation du système sont à l'origine d'un biais sur l'estimation. On peut également citer l'existence d'une erreur systématique sur un capteur ( exemple tension díoffset qui síajoute à la mesure ).
É
Le qualifiquatif au mieux suppose au sens díun critère . Le critère retenu est la minimisation de la variance de líerreur díestimation. Soit L la variance de líerreur díestimation,
![]() Détermination du gain de Kalman
Détermination du gain de Kalman
Le problème consiste à déterminer la matrice L qui minimise la variance de líerreur díestimation. Pour cette démonstration on exploite largement les résultats sur les processus markoviens démontrés en annexe.

Cíest líéquation díun processus Markovien, on a :

Pour déterminer la valeur de L* de L qui minimise L, ( soit L*cette valeur ), on pose :
L = L* + dL et L = L* + dL
dans líéquation de la variance de líerreur díestimation.
![]()
dont la solution est díaprès les résultats précédents:
![]()
Chercher L qui rende la variance de líerreur díestimation minimale veut dire que toute variation
dL autour de L* doit engendrer une variation dL positive.
Figure 12
Pour obtenir cela, il faut :
- initialiser le filtre de façon optimale, i.e. avec L(t0) minimale, alors dL(t0) > 0
- choisir :
|
|
ainsi, le terme qui apparaît sous líintégrale est nul. quelque soit dL.
En reportant :
![]()
dans líéquation de dL / dt, il vient :
|
|
C'est une équation de Riccati
à intégrer avec la condition initiale
L(t0).Remarque 1
:
Remarque 2
: La condition initiale L(t0) dépend de la connaissance que líon a a priori de líétat du système. On peut néanmoins díaprès la connaissance initiale que líon a du système chercher líétat initial estimé![]()
Et,

S
0 est la variance de líétat initial, matrice strictement positive, le second terme est une matrice de variance, également positive quíon peut au mieux annuler. L0 est minimale et égale à S0 pourRemarque 3
: Le filtre de Kalman ne fonctionne que síil y a du bruit de mesure. Autrement dit, R doit être définie positive ( elle admet alors une inverse ).Remarque 4
: Il peut arriver que L(t) diverge, auquel cas, il faut réinitialiser le filtre.Remarque 5
: On pourrait établir la dualité entre le problème de líobservateur optimal et le problème de la commande optimale.Soit un module "retour sur terre" dont on cherche à estimer la vitesse lors de sa traversée de l'atmosphère.
Figure 14
Equations du système
: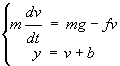
Seule la mesure de la vitesse est bruitée. Le bruit b(t) est blanc, gaussien, centré et de variance égale à r≤,
On note S la variance de l'état vitesse,
L
la variance de l'erreur d'estimation.L'état initial est connu avec une espérance égale à 15 m/s et une variance S0 ,
Pour simplifier, le véhicule est de masse unitaire.
On cherche le filtre de Kalman qui minimise líerreur díestimation de la vitesse.
Identification : A = -f, C = 1, R = 1, Q = 0
Remarquons que la variance de l'erreur d'estimation à l'instant initial L0 est inconnue , elle est au moins égale à S0 d'après la remarque 2.
Equation de la variance de líerreur díestimation :
![]()
Equation du gain de Kalman :
![]()
Tous calculs faits :
![]()
Remarquons que lorsque t ® + • le gain de Kalman devient stationnaire L = 2.f.
Equation d'évolution de l'estimation :

Plusieurs cas sont étudiés.
Première simulation
L'état initial est connu par sa moyenne égale à 18 m/s et sa variance égale à 1. Ces valeurs sont obtenues par l'expérience qu'on a des phénomènes étudiés, par les modèles qu'on a établis etc. D'après la remarque 2, on fixe l'état initial estimé à 18 m/s.
L'état initial réel vaut en fait 20 m/s, l'estimation initiale doit cependant être correcte car l'état réel est cerné dans un intervalle de +/- 3s0 autour de la moyenne ( s0 désigne l'écart type, racine carré de la variance ).
Interprétation des résultats : Le filtre est correctement initialisé, rapidement, le gain de Kalman tend vers 0, il fait confiance à l'estimation ; puisqu'il n'y a pas de bruit d'état, il ne sert à rien de faire des mesures si ce n'est à ajouter des erreurs !
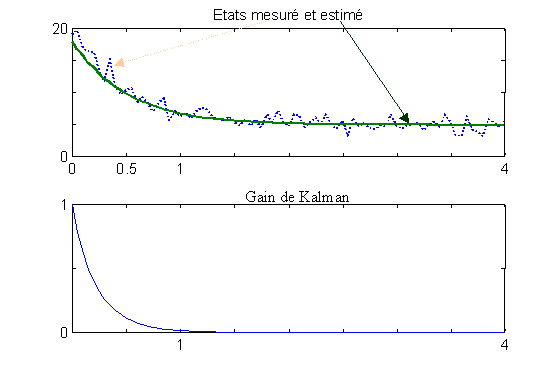
Figure 15
Seconde simulation
L'état initial est connu par sa moyenne égale à 18 m/s mais cette valeur est très incertaine aussi sa variance est choisie égale à 100. Lors de la simulation, on fixe la valeur de l'état initial estimé à 50 m/s ( On remarquera qu'on est à la limite supérieure de l'intervalle de confiance +/- 3 s0 ).
L'état initial réel vaut en fait 20 m/s.
Interprétation des résultats : Le filtre est correctement initialisé, le gain de Kalman est important ( 100 ), il fait confiance à la mesure. Celle-ci permet dans un premier temps de cerner correctement la valeur de l'état ( L'état estimé tend rapidement vers l'état réel). Aussi, dans un second temps, le filtre ayant "rattrapé l'erreur", il est possible de faire confiance à l'estimation puisqu'il n'y a pas de bruit d'état ( gain de Kalman égal à 0 ).
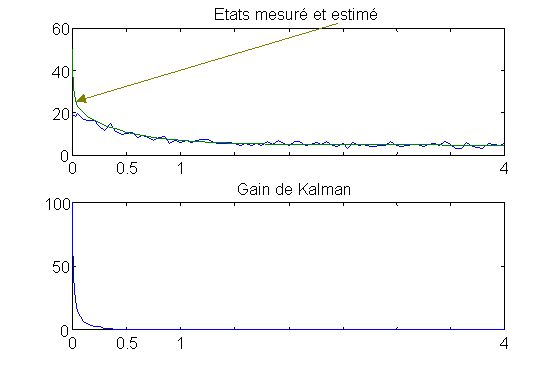
Figure 16
Simulation 3
Dans cette simulation, le filtre est mal initialisé, on suppose bien connaître l'état initial qu'on fixe à 50, bien connaître l'état initial cela suppose une faible variance, on choisit S0 égale à 1. En fait l'état initial réel est égal à 20.
Interprétation des résultats : Le filtre lors de l'initialisation fait confiance à l'estimation ( variance initiale petite ), or celle-ci est complètement erronnée, ce qui explique le temps relativement long mis pour rattraper l'erreur ).
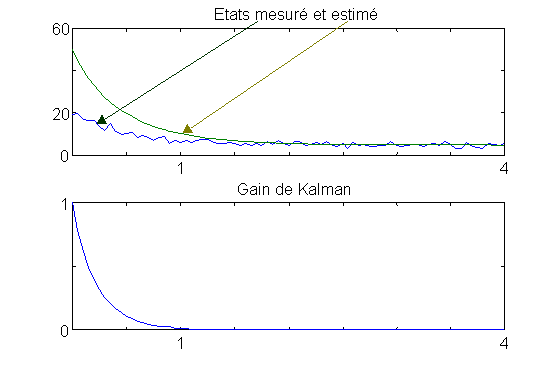
Figure 17