Lors du chapitre précédent on a établi la méthode permettant díélaborer une loi de commande optimale u* qui minimise le critère :
![]()
Pour un système décrit par sa représentation díétat :
![]()
La commande optimale u* a été élaborée pour un système en boucle ouverte
![]() Inconvénients de la boucle ouverte
Inconvénients de la boucle ouverte
Les systèmes ainsi commandés sont très sensibles aux perturbations et aux variations du modèle. La contre-réaction (i.e. bouclage des états sur les entrées ) améliore considérablement les performances du système vis à vis des perturbations. On cherche à réaliser la commande optimale u* à partie des entrées et des états du systèmes.
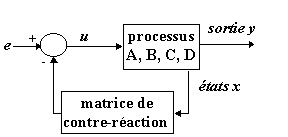
Figure 1
- Le système est commandable.
On cherche à élaborer une loi de commande qui soit linéaire par rapport aux états ![]() , par conséquent,
, par conséquent,
- Le système est linéaire,
- Le critère est quadratique :
![]()
Díoù líappellation L(inéaire)Q(uadratique).
En effet, lorsquíon écrit les équation de Hamilton pour élaborer la commande optimale, on résoud Hu=0. Le gradient est alors une forme linéaire en u.
Dans ce cours, deux types de problèmes sont envisagés :
![]() Problème de régulation : On cherche à maintenir les états autour de 0. Le système peut être soumis à des perturbations qui affectent les états. Líobjectif est díélaborer la commande optimale u* qui minimise le critère J en présence de perturbations.
Problème de régulation : On cherche à maintenir les états autour de 0. Le système peut être soumis à des perturbations qui affectent les états. Líobjectif est díélaborer la commande optimale u* qui minimise le critère J en présence de perturbations.

Figure 2
![]() Problème de poursuite : Les états doivent suivre une trajectoire de consigne Xc, il faut établir la loi de commande optimale qui minimise le critère.
Problème de poursuite : Les états doivent suivre une trajectoire de consigne Xc, il faut établir la loi de commande optimale qui minimise le critère.
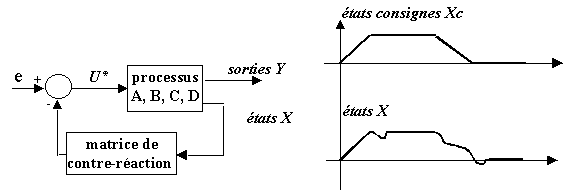
Figure 3
![]()
- Le critère quadratique :
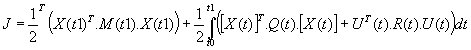
Cíest un problème classique de minimisation que líon traite avec les équations de Hamilton. Líobjectif est díétablir une relation de la forme :
![]()
Ā
Hamiltonien![]()
Pour applique le principe du minimum, on utilise les propriétés suivantes de la dérivation partielle vectorielle.
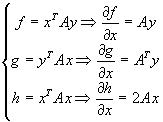
ā
Equations de Hamilton![]()
![]()
É
On réinjecte la commande optimale dans líéquation díétat![]()
Ą
On a alors un système díéquation différentielle sans second membre en X et en m†
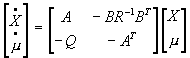
†

Figure 4
Ö
On intègre ce système díéquations en tenant compte du coût terminal auquel il faut appliquer la condition de transversalité ( cf. chapitre V, ß ) :![]()
$
On rappelle que líintégration de líéquation díétat fait intervenir la matrice de transition ( qui possède la propriété de transitivité ).![]()
Compte tenu de la propriété de transitivité, on peut exprimer Z(t) depuis un nouvel état initial Z(t1). On a :
![]()
On exploite cette propriété pour intégrer X et m à partir des informations disponibles qui portent sur líinstant final. Ces équations síintègrent à rebours.
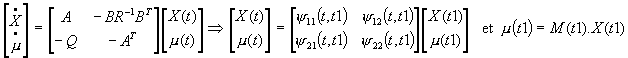
La matrice de transition est de dimension ( 2n x 2n ).
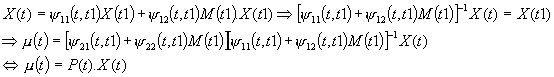
Ce dernier résultat porté dans les équations díétats et de Hamilton :
![]()
![]()
P
P est fonction du tempsIl reste à déterminer P(t), comme
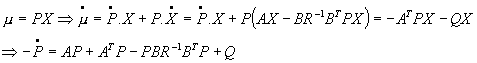
avec la condition terminale :
![]()
Remarque : P(t) est symétrique, définie semi-positive et son inverse et solution de líéquation de Riccati.
On en déduit líexpression de la matrice de contre réaction K(t), comme :
![]()
La structure de la commande linéaire quadratique :

|
|
Figure 5
Lors de la réalisation de la commande, il est nécessaire díintégrer P à rebours avant díimplanter K(t). De plus, il convient de remarquer que la matrice de contre-réaction níest pas stationnaire ( dépendance vis à vis du temps ). Cíest une difficulté majeure dans la réalisation de la commande.
Remarque :
P(t) est symétrique, définie semi-positive et son inverse est solution de líéquation de Riccati.
On montre que la seconde variation de J est positive ( condition suffisante de minimum) car les matrices M, Q semi-positives et R positive.
On se propose dans cet exemple de mettre en úuvre une commande linéaire quadratique et de comparer les résultats obtenus ceux fournis par une commande optimale en boucle ouverte.
Le système étudié est un véhicule de masse m unitaire dont on veut maintenir la vitesse v(t) autour díune vitesse de consigne vc constante. Ce système est décrit par líéquation díétat : ![]() avec la condition initiale v(0) = 0
avec la condition initiale v(0) = 0
- le critère à minimiser : ![]() réalise un compromis entre la minimisation de líerreur le long de la trajectoire et líénergie dépensée.
réalise un compromis entre la minimisation de líerreur le long de la trajectoire et líénergie dépensée.
- le vecteur díétat choisi est líerreur de vitesse, x = v - vc quíil faut maintenir autour de 0. Cíest un problème de régulation.
![]()
où :
![]()
- La commande optimale a pour solution :
![]()
- La matrice de Riccati est solution de :
![]()
Résolution de líéquation de Riccati à rebours : tr = t1 Ė t :
![]()
- la condition terminale :![]()
![]()
Les chronogrammes suivants représentent successivement la commande optimale, líétat erreur de vitesse et la solution de líéquation de Riccati pour q = 5 puis q = 1. Dans le premier cas, on privilégie le rattrapage de líerreur, objectif atteint au prix díune forte sollicitation de la commande. Dans le second cas, on atteint le même résultat moins rapidement ; en revanche, líénergie mise en jeu est moindre. On notera également que la solution de líéquation de Riccati pour tr suffisament grand tend vers une valeur stationnaire qui est la solution positive du second membre de líéquation de Riccati. En annexe, on trouvera les résultats relatifs au même système dont la loi de commande en boucle ouverte a été établie avec les équations de Hamilton.

![]() SYSTEME ET CRITERE STATIONNAIRE A HORIZON INFINI
SYSTEME ET CRITERE STATIONNAIRE A HORIZON INFINI
Pratiquement, la difficulté de la réalisation réside dans líintégration à rebours de líéquation de Riccati et dans líimplantation de la commande K(t)= R-1.BT.P(t) qui doit être menée avant que le processus démarre. De plus, la commande dépend du temps. Líexemple montre que la loi díévolution de K(t) est stationnaire sur une plage importante et quíelle tend vers la solution positive du second membre de líéquation de Riccati. On síaffranchit des conditions terminales en élaborant une commande sur horizon infini. Ce résultat est significatif si líhorizon díétude est grand devant les constantes de temps du système.
La commande optimale qui minimise le critère
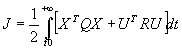 Q, R = Cte
Q, R = Cte
fait appel à une matrice de contre réaction ![]() indépendante du temps.
indépendante du temps.
U*(t) = -![]() X(t)
X(t) ![]() =R-1.B.
=R-1.B. ![]() la matrice
la matrice ![]() définie semi-positive est solution de l'équation :
définie semi-positive est solution de l'équation :
|
|
La commande est beaucoup plus facile à réaliser que dans le cas à horizon fini, en effet, elle ne dépend plus du temps.
Les chronogrammes suivants mettent en évidence líeffet díune commande LQ sur horizon infini pour le système étudié lors de l'exemple précédent. Les réponses obtenues sont quasi-identiques pour une commande beaucoup plus simple à réaliser.

Figure 7
Les états sont astreints à suivre une trajectoire de consigne. Le critère a pour expression :
![]()
où Xc désigne la trajectoire de consigne.
On raisonne comme dans le cas de la régulation,
Ā
Hamiltonien![]()
ā
Equations de Hamilton![]()
![]()
É
On réinjecte la commande optimale dans líéquation díétat![]()
On a alors un système díéquations différentielles non homogènes en X et en m traduites sous forme de schéma figure 6.
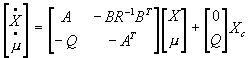
On exploite la condition de transversalité portant sur le coût final,
![]()
Les équations sont à intégrer à rebours comme dans le cas de la régulation. On cherche une solution de la forme :
![]()
On aboutit à ce résultat en utilisant la matrice de transition, attention, líéquation comporte un second membre.
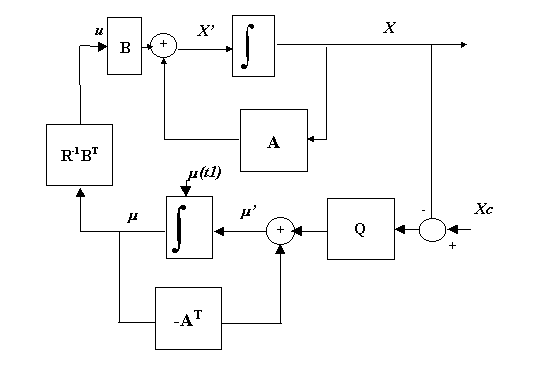
Figure 8
Ą
On porte líexpression de m(t) dans les équations díétat et les équations des multiplicateurs de Lagrange :![]()
![]()
![]()
![]()
Cette dernière équation est vérifiée quelque soit líétat X. On retrouve líéquation de Riccati ![]() dont la matrice P fournit la commande par retour díétat dans le cas díun problème de régulation . Il faut de plus intégrer líéquation
dont la matrice P fournit la commande par retour díétat dans le cas díun problème de régulation . Il faut de plus intégrer líéquation ![]() qui correspond au régime forcé lié au problème de poursuite.
qui correspond au régime forcé lié au problème de poursuite.
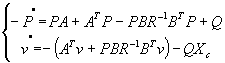
Ces équations sont à intégrer avec les conditions terminales :
![]()
![]() .
.
Ces deux équations síintègrent à rebours puis sont implantées sur le correcteur ; ce qui pose des difficultés lors de la réalisation.
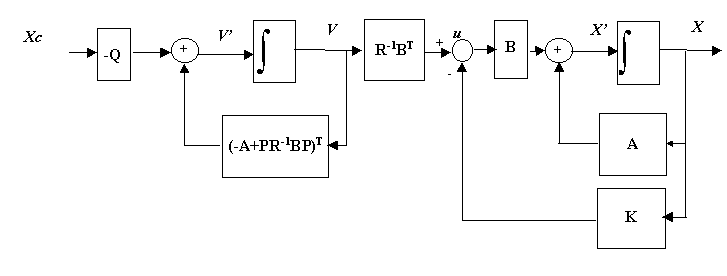
Figure 9
On reprend líexemple précédent. On désire maintenir líétat vitesse autour díune consigne vitesse vc constante tout en minimisant la consommation díénergie. Cíest un problème analogue au précédent excepté dans le choix du vecteur díétat qui doit être maintenu autour de vc ( problème de poursuite ) et non plus autour de 0 ( problème de régulation ). Pour rendre évidente la notion de préfiltre, on traite ce problème sur horizon infini.
Ā
Equation du régulateur : K = -qā
Equation du préfiltre :![]()
On suppose le régime permanent atteint ( Rappelons quíil faut intégrer à rebours et que líorigine des temps est líinstant final quíon fait tendre ici vers + • )
Þ ![]()
comme
![]()
Le gain du préfiltre vaut -q.
Ce résultat était prévisible. On a établi dans le cours díasservissements linéaires que le gain statique díun système en boucle fermée était égal à ![]() soit
soit ![]() dans líexemple étudié. Pour un problème de poursuite, on cherche à obtenir un gain en boucle fermée unitaire ; il convient donc de multiplier la consigne par Ėq.
dans líexemple étudié. Pour un problème de poursuite, on cherche à obtenir un gain en boucle fermée unitaire ; il convient donc de multiplier la consigne par Ėq.