![]() Rappels sur le calcul des variations
Rappels sur le calcul des variations
Le chapitre précédent a mis en évidence la notion de critère ou fonction de coût, expression analytique qui vise à conférer à un système certaines performances. Líobjectif de ce cours est líélaboration díune loi de commande optimale u* qui minimise un critère J. Le système est décrit par une équation díétat.
Líexpression du critère : ![]()
Equation díétat du système : ![]()
Il síagit díun problème de minimisation, rappelons quelques résultats utiles.
Une fonction f(x) admet un minimum au point x* si elle vérifie :
![]()
Le critère J à minimiser est une fonction de plusieurs variables. Les conditions de minimum peuvent être établies à partir de son développement de Taylor :
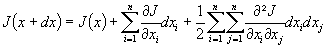
On utilise avantageusement líécriture matricielle, comme

en posant Le gradient de J par rapport à x,
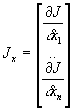
et le hessien
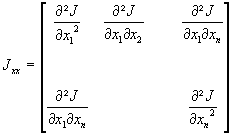
il vient : 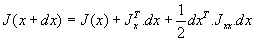
On peut dès lors établir les conditions de minimum :
Jx = 0 " dx
Jxx > 0 " dx
Remarque : Une matrice est définie positive lorsque elle vérifie : xT.A.x > 0 " x
Le problème à résoudre est différent. Dans líexpression du critère , líévolution du vecteur díétat x níest pas libre, elle est assujettie à líéquation díétat ![]() . On dit encore quíelle est contrainte. Il síagit là díun problème de minimisation sous contraintes quíillustre líexemple suivant.
. On dit encore quíelle est contrainte. Il síagit là díun problème de minimisation sous contraintes quíillustre líexemple suivant.
Soit à minimiser la fonction ![]() , sous la contrainte
, sous la contrainte ![]() . Il síagit simplement ici de mininimiser la distance OP.
. Il síagit simplement ici de mininimiser la distance OP.

Figure 1
La méthode qui suit permet de se ramener à un problème de minimisation classique i.e. sans contrainte. Considérons une fonction J(x) contrainte par g(x) = 0 " x , dans le cas où il y a p contraintes, on la note g(p)(x) = 0.
On a pour tout x et en particulier en x*:
g(p)(x* + dx ) Ė g (p) ( x* ) = 0 Û gx (p)(x*).dx = 0
Comme au point x* les p gradients gx(p)(x*) ne sont pas nécessairement nuls, ils sont orthogonaux à dx.
Par ailleurs la condition de minimum Jx(x*) = 0 valable sans contrainte níest plus vérifiée. Il faut considérer la condition de minimum sous sa forme complète i.e.
Jx(x*).dx = 0 Þ dx orthogonal à Jx(x*), dx níest pas quelconque.
Jx(x*) et les p vecteurs gradients gx(p)(x*) sont orthogonaux aux dx. On peut écrire Jx(x*) comme une combinaison linéaire des gx(p)(x*).
Jx(x*) + ![]() mi.g(p)x(x*) = 0 Û Jx(x*) + mT.g(p)x(x*) = 0 ,
mi.g(p)x(x*) = 0 Û Jx(x*) + mT.g(p)x(x*) = 0 ,
Avec m = [ m1, Ömp ]T où les mi sont les multiplicateurs de Lagrange.
On se ramène à un problème de minimisation sous contraintes à un problème de minimisation sans contrainte en introduisant le hamiltonien H(x, m ,t )
H(x, m, t) = J(x) + mT.g(p)(x)
Rechercher le minimum de J(x) sous les p contraintes g(p)(x) = 0 est équivalent à rechercher le minimum de H sans contrainte. Avec les variations de x et de m indépendantes ; en effet :
Hx(x*) = Jx(x*) + mT.gpx(x*) = 0 n relation qui fournissent x*(m).
Hm = g(p)(x) = 0 fournit p relations qui donnent m
Il faut en toute rigueur vérifier Hxx > 0.
On résout líexemple précédent. Ecrivons le hamiltonien :
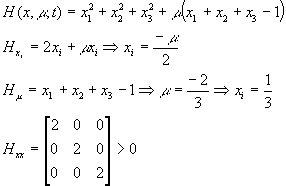
On Remarque quíen x* on a 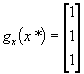 colinéaire à
colinéaire à 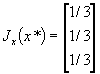 ( problème à une seule contrainte ) et que dx est porté par le plan díéquation g(x) = 0.
( problème à une seule contrainte ) et que dx est porté par le plan díéquation g(x) = 0.
![]() Application au problème de la commande optimale
Application au problème de la commande optimale
On cherche à établir la commande optimale u* qui minimise le critère :
![]()
soit J* la valeur minimale du critère.
Líévolution des n états , est soumise aux n contraintes ![]() quíon met sous la forme
quíon met sous la forme ![]() .
.
Le critère peut encore síécrire :
![]()
Pour se ramener à un problème de minimisation sans contrainte on introduit le hamiltonien :
![]()
![]()
On intègre par partie le second terme sous líintégrale,
![]()
Pour un système partant de líétat initial x(t0) à líinstant t0 et devant atteindre líétat final x(t1) à líinstant t1, le minimum du critère, J* est obtenu pour la commande optimale u*. Comme on cherche à minimiser J, on va créer une petite variation dJ autour de J* et on cherchera les conditions pour lesquelles dJ síannule. Pratiquement cela revient à faire varier ce que líon peut et à en évaluer les conséquences sur la trajectoire díétat et la fonction de coût.
Quels sont les paramètres susceptibles de faire varier la trajectoire díétat et par suite le critère ?
- Líinstant initial et líinstant final : t0 + dt0 , t1 + dt1 ( le système ne " démarre " pas tout à fait à líinstant souhaité et ne parvient pas à líétat final dans les temps imposés, ces variations peuvent avoir pour origine des retards non pris en compte, des perturbations etc. )
- Les conditions initiales et finales : x0 + dx0 , x1 + dx1 ( sous líeffet de perturbations aux instants t0 et t1, líétat initial et líétat final sont différents des états désirés )
- La commande u* + du ( la commande réelle appliquée au système diffère de la commande calculée, cette variation peut avoir pour origine le bruit de quantifiquation dans le cas díune commande numérique, des dérives sur les alimentations díun amplificateur de puissance générant la commande u, etc. )
Par hypothèses, ces variations sont supposées être toutes indépendantes
.Remarque : Dans la plupart des problèmes posés, líinstant et líétat initial sont imposés dx0 = dt0 = 0.
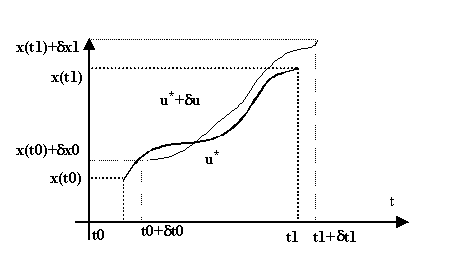
Trajectoire optimale et trajectoire perturbée
Figure 2
Pour déterminer dJ, on a besoin de deux résultats intermédiaires :
Ā
ā
On calcule dJ puis on sépare les effets propres à chacune des variations supposées indépendantes.
|
|
|
|
|
+ |
|
+ |
|
+ |
|
+ |
Dans un premier temps on suppose les instants et les états terminaux parfaitement imposés, les variations associées dt0, dt1, dx0, dx1 sont nulles. La condition de minimum porte le long de la trajectoire et J est minimum si :
|
|
$
On exploite ici le lemme de Lagrange ; Si y(t) est une fonction continue sur [t0, t1] et si :![]() Principe du minimum de Pontryaguin
Principe du minimum de Pontryaguin
Les équations de Hamilton déterminées au paragraphe précédent fournissent la loi de commande qui minimise le critère le long de la trajectoire díétat.
|
|
|
|
|
|
Dans la pratique, des contraintes sur la commande rendent parfois impossible líélaboration de u*.
Díune manière plus générale et pour prendre en compte ces cas particuliers, Pontryaguin a énoncé le principe suivant :
La commande ( u* ![]() ) qui minimise le critère
) qui minimise le critère
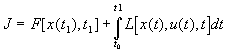
sous la contrainte ![]()
est telle que la fonction de Hamilton H = L + mT.f soit minimale :
|
H(x*, u, m, t ) |
Et ![]()
![]()
Remarque : Un cas fréquent díapplication du principe concerne les hamiltonien linéaires par rapport à la commande u alors que celle-ci est contrainte d1£ u£ d2. Líhamiltonien síécrit : H = a(t).u + b(t).
On discute des variations de a(t) sur [t0, t1] afin díétablir son signe,
a
> 0 Þ H minimum si u = d1a
< 0 Þ H minimum si u = d2Les équations de Hamilton précitées constituent une condition nécessaire de minimum pour le critère J. Elles permettent díélaborer la loi de commande optimale u*. Il reste quíil faut tenir compte des variations sur les états terminaux dt0 , dt1 , dx0 , dx1 pour intégrer les équations díétats. Le tableau page 8 envisage les cas les plus fréquents.
Remarque : Lorsque líinstant final t1 est libre et que la fonction F ( coût terminal ) ne dépend pas du temps, le hamiltonien est nul à líinstant t1. Il est nul sur toute la trajectoire si le critère est invariant dans le temps.
|
Cas rencontrés |
Données |
|
Instants initial et final imposés Etats initial et final imposés |
d t0 = dt1 = dx0 = dx1 = 0Ā Hu = 0 è u*(m)ā Hx = -mí è m è u*É u* dans+ n conditions initiales + n conditions finales |
|
Instants initial et final imposés Etat initial imposé, final libre |
d t0 = dt1 = dx0 = 0 , dx1 Ļ 0Ā Hu = 0 è u*(m)ā Hx = -mí è m è u*É Ą + n conditions initiales + n conditions extraites de É |
|
Instants initial imposé, final libre Etats initial et finaux imposés |
d t0 = dx0 = dx1 = 0 , dt1 Ļ 0Ā Hu = 0 è u*(m)ā Hx = -mí è m è u*É Ą u* dans+ n conditions initiales + n conditions finales |
|
Instants initial et final imposés Etats initiaux et finaux libres |
d t0, dx0 = 0 ; dx1, dt1 Ļ 0Ø Combiner les conditions de transversalité précédentes. |
![]() Calcul de líhamiltonien sur la trajectoire optimale
Calcul de líhamiltonien sur la trajectoire optimale
Le calcul de la dérivée totale de líhamiltonien par rapport au temps :
![]()
est égale à la dérivée partielle car Hu = 0, Hm = ![]() et
et ![]() Þ
Þ ![]() le long de la trajectoire optimale.
le long de la trajectoire optimale.
Comme H = L + mT.f, si le critère et le système ne dépendent pas explicitement du temps Þ ![]() et líhamiltonien est constant sur toute la trajectoire. Si de plus, le temps final est libre, H[x*(t1), u*(t1), m(t1) ] = 0, on en déduit que líhamiltonien est nul sur toute la trajectoire. Ce résultat fournit une équation supplémentaire exploitable lors de la recherche díune loi de commande optimale.
et líhamiltonien est constant sur toute la trajectoire. Si de plus, le temps final est libre, H[x*(t1), u*(t1), m(t1) ] = 0, on en déduit que líhamiltonien est nul sur toute la trajectoire. Ce résultat fournit une équation supplémentaire exploitable lors de la recherche díune loi de commande optimale.
On cherche à réaliser une loi de commande qui minimise la distance de freinage d díun avion lors de líatterrissage tout en minimisant le coût énergétique. On níutilise que la reverse moteur, les effets aérodynamiques sont négligés.
Le critère à minimiser :
![]()
Líappareil de masse M égale à 10 tonnes se présente au sol à líinstant t0 = 0 en x(t0) = 0 avec une vitesse v0 égale à 50 m/s, la manette des gaz permet de créer une force de freinage u.
Le critère représente un compromis entre la distance de freinage x(t1) et líénergie dépensée.
Ā
Conditions terminalesā
Equations díétat avec : x(t) = x1(t) et v(t) = x2(t)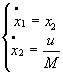 Þ 2 contraintes Þ m = [ m1(t) , m2(t) ]T
Þ 2 contraintes Þ m = [ m1(t) , m2(t) ]T
É
Hamiltonien![]()
Ą
Equations de HamiltonLa commande u níest pas contrainte, ![]() (1)
(1)
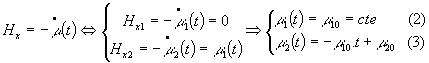
Ö
Conditions de transversalité- état position finale libre : Fx[ x1(t1) , t1 ] = m1(t1) Þ m.x1(t1) = m1(t1)
comme díaprès (2), m1(t) = cte Þ m10 = m.x1(t1) = m.d
![]() Þ
Þ ![]()
díaprès (1) Þ ![]() (4)
(4)
(4) dans (3) ![]() díoù :
díoù : ![]()
Ü
Intégration des équations díétat![]() comme
comme ![]()
On exploite les conditions terminales à t = 0:
x1(0) = 0 Þ ![]()
x2(0) = v0 Þ ![]()
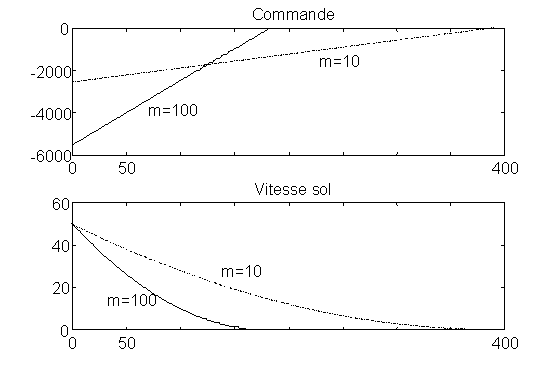
Figure 3