MISE EN EVIDENCE
Illustration des notions de commandabilité et d'observabilité
Considèrons le cas d'une automobile vu comme processus. L'accélérateur est supposée être la seule commande de ce système, sa vitesse la grandeur de sortie. Les états considérés sont :
- Vitesse de rotation du moteur,
- Niveau de charge des batteries; le moteur entraînant l'alternateur,
- La masse du véhicule,
- L'état d'un phare ( allumé ou éteint ).
L'action sur l'accélérateur permet de contrôler les trois premiers états, ils sont commandables.
La connaissance de la vitesse du véhicule et de la commande appliquée permettent d'extrapoler celle du moteur. Cet état est observable. De même, il est possiblet de déterminer la masse de l'automobile qui obéit à la relation fondamentale de la dynamique. Cet état est également observable.
L'état d'un phare est indépendant de l'action sur la pédale d'accélérateur, cet état est non commandable.
La vitesse du véhicule et la position de la pédale de l'accélérateur ne nous renseignent; ni sur l'état du phare, ni sur le niveau de charge de la batterie qui sont des états inobservables.
Soit le système décrit par les équations d'état :
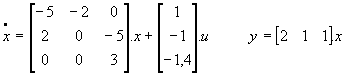
Les états sont couplés entre eux, il n'est pas possible de conclure quant aux effets de la commande sur les états. A cause de ces mêmes couplages, les états peuvent avoir des effets antagonistes sur la sortie.
Ce processus admet une représentation sous forme diagonale ( chapitre I, § 4 et 5.1).
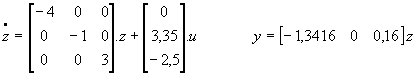
La représentation d'état sous forme diagonale ( et elle seule ) permet de conclure immédiatement quant à la commandabilité et l'observabilité d'un processus. Les états étant découplés, on peut remarquer que la commande agit sur les états z2 et z3, ces états sont commandables. En revanche, elle n'a aucun effet sur l'état z1. cet état est non commandable. On notera que le mode correspondant au troisième état est instable.
La sortie y est une combinaison linéaire des états z1 et z3. De fait, la connaissance de la sortie y et de la commande u appliquée au processus doit permettre de retrouver ces états, on dit qu'ils sont observables. La sortie y ne contribue pas à la connaissance de l'état z2. Cet état est inobservable.
Figure 1
Un processus de vecteur d'état X(t) est complètement commandable sur l'intervalle de temps [ t0, tf ] s'il existe sur cet intervalle une commande U(t) permettant d'amener ce vecteur d'un état initial quelconque X(t0) à un état choisi quelconque X(tf).
Dans le cas d'une représentation d'état quelconque, le critère suivant permet de conclure quant à la commandabilité.
L'évolution du processus est décrite par l'équation d'état : 
dont on a établi la solution :
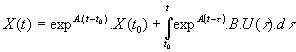
Qui compte-tenu de la formule de Sylvester 
établie au chapitre précédent peut s'écrire :
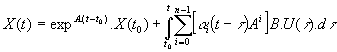
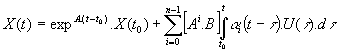
Soit sous forme matricielle :
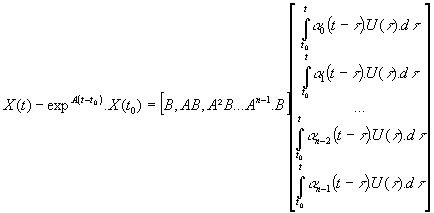
Ce système admet n états solutions , pour être résolvable il faut n équations linéairement indépendantes, ce qui implique :
rang
[ B, AB,A²B...An -1.B ] = n [ B, AB, …] est la matrice de commandabilitéOn rappelle que le rang d’une matrice donne le nombre maximum de lignes indépendantes et le nombre maximum de colonnes indépendantes.
Exemple
Appliqué au processus du § 1.2, on montre que le système est de rang 2. On montre que Col3 = 3.Col1 + 2.Col2
[ B, AB, A²B ] =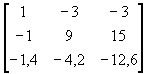 
et det[ B, AB, A²B] = 0
Un système est dit complètement observable sur l'intervalle de temps [ t0, tf ] si l'observation de la commande U(t) et de la sortie Y(t) permet de déterminer l'état initial X(t0).
Dans le cas d'une représentation d'état quelconque, le critère suivant permet de conclure quant à l'observabilité.
L'évolution et l'observation du processus sont décrites par les équations :
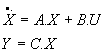
dont la solution a été établie au chapitre précédent,
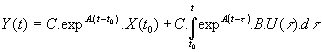
en utilisant la formule de Sylvester, cette relation s'écrit :
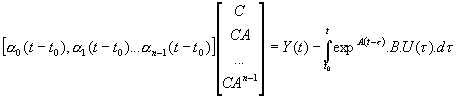
On exprime cette relation pour n valeurs de t, on obtient un système linéaire dont la résolution est soumise à la condition :
|
rang |
Exemple
Reprenons l'exemple développé au §1.2, le critère confirme la non observabilité du processus.
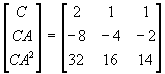et 
La mesurabilité et l'observabilité sont deux notions distinctes.
Pour mesurer un état, il suffit théoriquement de disposer d'un capteur adéquat. Encore faut-il que sa mise en oeuvre soit possible, on parle alors d'état mesurable, sinon l'état est dit non-mesurable. Un état peut être non mesurable pour des raisons technologiques ( problème du poids des capteurs et de leur chaîne de traîtement en aéronautique, problème de l'accés à la mesure du flux dans un moteur ) ou économiques.
Cependant, la volonté de diminuer les coûts de fabrication, les contraintes liées à la présence de capteurs, les progrès de l'informatique et de l'électronique amènent de plus en plus les concepteurs à remplacer les capteurs et leur chaîne d'aquisition par des reconstructeurs d'états. L'idée consiste à exploiter l'ensemble des informations disponibles ; la sortie y mesurée et la commande u du processus. Si le traitement de ces informations permet de reconstruire tout ou partie des états, le système est observable.
Dans le cas le plus général un processus peut-être décomposé en quatre sous-systèmes :
: Système commandable et observable,
:
: Système non commandable et observable,
: Système non observable et non commandable.
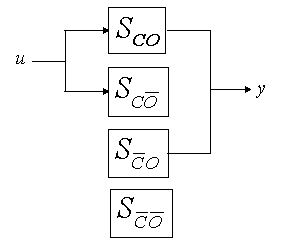
Figure 2
Il apparaît immédiatement que la fonction de transfert 
(représentation externe) perd les modes non commandables et non observables. De fait, les pôles sont les modes associés aux états commandables et observables.
STABILISABILITE - DETECTABILITE - GOUVERNABILITE
Pour commander un processus on peut :
ð
En boucle ouverte, appliquer sur l'entrée une commande avec un profil adéquat qui confère aux états et aux sorties les performances souhaitées. Cette méthode présente l'inconvénient d'être sensible aux perturbations.ð
Reboucler les états sur l'entrée pour générer le signal de commande. Cette stratégie présente l'avantage d'être beaucoup moins sensible aux perturbations que la précédente. Dans le cas de la commande par retour d'état, il faut reboucler tous les états.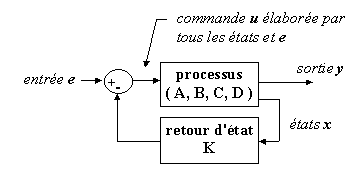
Figure 3
En pratique, il n'y a pas de moyen d'action sur les parties non commandables du système. Si ces parties sont stables, sous l’effet de perturbations, les variables d'état qui les caractérisent tendent vers zéro, chacune avec sa dynamique propre. Par contre, si elles sont instables, il apparaît un risque de détérioration du matériel. Un système est dit stabilisable si ses modes instables sont commandables. On peut alors élaborer un signal de commande qui empêche l'état de diverger. C'est une condition nécessaire pour rendre le système stable, elle n'est pas suffisante.
Observation des états instables
Pour élaborer la commande il faut disposer de tous les états. Or la seule information à laquelle on a généralement accés est la sortie. Si le système est observable, la connaissance de la sortie et de la commande permettent de reconstruire tous les états. Les états instables doivent être nécessairement observables. On dit des états instables observables qu'ils sont détectables.
Lorsque les modes instables sont stabilisables et détectables, le système est gouvernable. L'exemple développé au § 1.2 est celui d'un système gouvernable.
Le test PBH ( Popov–Belevitch–Hautus ) permet d’identifier les modes non-commandables et inobservables.
Test de commandabilité
Pour un système d’ordre n, un mode est commandablee si et seulement si il vérifie :
Test d’observabilité
Pour un système d’ordre n, un mode est observable si et seulement si il vérifie :
Exemple
Reprenons l’exemple du 1.2, et testons la commandabilité du mode –1. On applique le test :
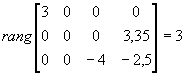ce mode est commandable
Appliquons le test au mode –4
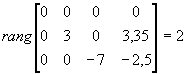ce mode est non-commandable.
