![]()
![]() NOTION D'ETAT
NOTION D'ETAT
La représentation d'état repose sur la notion d'énergie. Un processus décrit sous forme de représentation d'état est caractérisé par ses variables d'états qui sont des facteurs d'énergie. Ces variables d'état donnent une description interne complète de l'évolution du système.
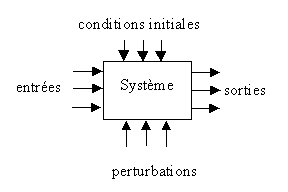
Figure 1
Cette démarche est naturelle puisque l'évolution d'un processus à un instant t0 donné dépend :
- de son "état énergétique" à cet instant t0.
- des sollicitations extérieures ( les commandes et les perturbations ).
Remarques :
- Le traitement a lieu dans le domaine temporel et fait appel à l'outil matriciel.
- Le cas multivariable peut être appréhendé.
Cet exemple simple va nous permettre d'illustrer les "concepts" de la théorie de la représentation d'état.
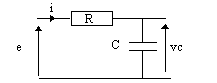
Figure 2
![]() Mise en équation
Mise en équation
Pour ce système, on choisit vc(t) comme variable d'état, en effet,
- vc(t) est un facteur d'énergie potentielle puisque ![]()
- la sortie observée est le courant ![]()
![]() ð équation qui traduit l'évolution de l'état
ð équation qui traduit l'évolution de l'état
![]() ð équation d'observation
ð équation d'observation
Lorsque ce système est soumis à un échelon d'heaviside d’amplitude e0, l'état et la sortie ont pour expression :
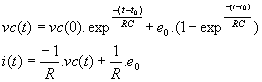
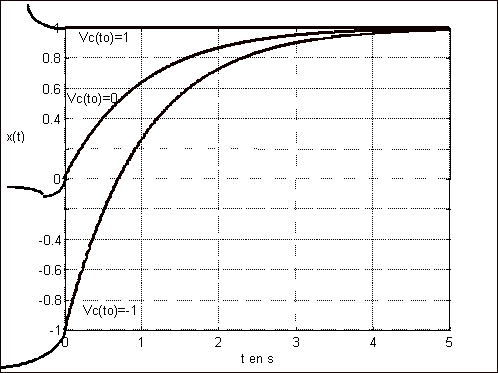
Figure 3
![]() Remarques :
Remarques :
L'allure de vc(t) sur l'intervalle [t0, t ] est indépendante de ce qui s'est passé avant t0 , vc(t) est la trajectoire d’état .
Si à l’instant t1 > t0 on applique une nouvelle commande, la sortie du système évoluera en fonction :
F du nouveau signal de commande
F de vc(t1), état à l'instant t = t1, mémoire minimale du système.
On peut enfin donner une représentation schématique de ce circuit RC,

Figure 4
![]() Interprétations
Interprétations
Cette illustration fait apparaitre une intégration qui équivaut à une accumulation d'énergie. Dans le cas étudié ![]() est au facteur C ( en farads ) près homogène à un courant. Le courant est un facteur d'énergie cinétique ; celle-ci est convertie par accumulation ( intégrateur ) en énergie potentielle avec comme facteur d'énergie vc(t). On choisit généralement les variable d'état à la sortie des intégrateurs.
est au facteur C ( en farads ) près homogène à un courant. Le courant est un facteur d'énergie cinétique ; celle-ci est convertie par accumulation ( intégrateur ) en énergie potentielle avec comme facteur d'énergie vc(t). On choisit généralement les variable d'état à la sortie des intégrateurs.
On observe également un transfert direct entrée-sortie, le terme en ![]() . Le respect du principe de causalité impose que ce transfert soit dissipatif ( résistance, frottement...).
. Le respect du principe de causalité impose que ce transfert soit dissipatif ( résistance, frottement...).
![]() Exemple : Moteur à courant continu
Exemple : Moteur à courant continu
Cet actionneur dont l'usage est très répandu de par l'extrême simplicité de sa commande va nous permettre d'illustrer le cas multivariables.
![]() Mise en équation
Mise en équation

Figure 5
![]() ð équation électrique
ð équation électrique
![]() ð équation mécanique
ð équation mécanique
Remarquons que i(t) est un facteur de l'énergie stockée dans l'entrefer sous forme électromagnétique et que W(t) est un facteur de l'énergie cinétique de rotation.
On fait alors apparaitre une représentation d'état en mettant ces équations sous la forme:
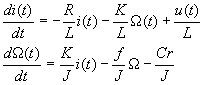
Ce qui, exprimé sous forme matricielle s’écrit :
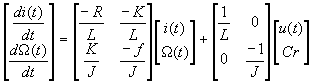 ð traduit l'évolution des états
ð traduit l'évolution des états
[ i(t) W(t) ]T est appelé vecteur d'état.
[ u(t) Cr ]T est appelé vecteur de commande.
On choisit comme grandeur de sortie la vitesse du moteur W(t), on peut alors écrire,
![]() ð équation d'observation
ð équation d'observation
On remarque qu'il n'y a pas de transfert direct entrée-sortie, un tel système est dit propre. On peut enfin établir une représentation du moteur à courant continu décrit par sa représentation d’état :
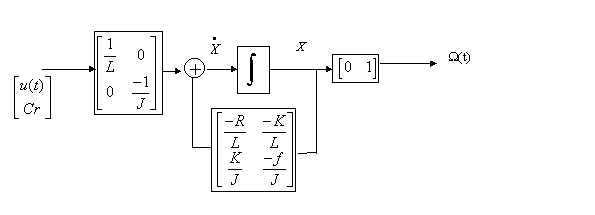
Figure 6
![]() Modèle externe - modèle interne
Modèle externe - modèle interne
La notion de fonction de transfert définie lors du cours d’asservissements linéaires continus nous informe sur la stabilité, la précision et la dynamique d'un processus physique. C'est un outil de représentation externe en ce sens où seules, la commande et la sortie apparaissent dans les équations. Le problème est traité dans le domaine fréquentiel et les conditions initiales sont nulles. La représentation d'état offre une description plus complète puisqu'elle permet de connaitre l'évolution des variables internes du processus. Celles-ci peuvent cependant être masquées pour l'utilisateur. Le concepteur doit en revanche prévoir leur évolution, et ce afin de garantir la viabilité du système.
Dans le cas d'un moteur à courant continu équipant une machine-outil, l'ouvrier gère la commande des axes de sa machine ( u(t) ) et observe la broche tourner W(t). Il ne lui est pas demandé de contrôler l'intensité du courant électrique ( l'autre variable d'état i(t)) pourtant responsable d'échauffements susceptibles de réduire notablement la durée de vie de son moteur. L'ouvrier a une connaissance externe de sa machine, l'ingénieur qui l'a conçue a envisagé ce problème et en a établi une représentation interne.
![]()
EQUATION D'ETAT, EQUATION D'OBSERVATION
Des exemples qui précèdent, on peut donner une écriture systématique pour les processus décrits par leur représentation d'état.
![]() ð équation d'état
ð équation d'état
![]() ð équation d'observation
ð équation d'observation

Figure 7
|
X est le vecteur d'état |
n*1 |
|
U est le vecteur de commande |
m*1 |
|
Y est le vecteur de sortie |
s*1 |
|
A est la matrice d'évolution des états ou matrice d’état |
n*n |
|
B est la matrice d'application de la commande ou matrice de commande |
n*m |
|
C est la matrice d'observation |
s*n |
|
D est la matrice de transmission directe ou matrice de couplage entrées-sorties |
s*m |
Dans de nombreux cas la matrice de transmission directe est identiquement nulle puisqu'elle représente le cas particuliers des liaisons qui sont la limite du principe de causalité.
FONCTION DE TRANSFERT
Il est possible de passer d'une description interne du système ( représentation d'état ) à une description externe ( fonction de transfert ). Le système est monovariable, les conditions initiales nulles, il est décrit par :

On applique à ces équations la transformée de Laplace,
![]()
![]()
|
|
Le polynôme caractéristique de A n'est autre que le dénominateur de la fonction de transfert. Les pôles de la fonction de transfert sont les valeurs propres de la matrice d'évolution des états A. Les valeurs propres de A conditionnent les performances dynamiques du processus.
Remarque : Dans le cas des systèmes multivariables, il existe des matrices de transfert.
![]() Exemple
Exemple
Soit le système décrit par la représentation d’état :

Calculons ( p.I - A ) -1 =

l'adjointe :
![]()
le déterminant :
det( p.I - A ) = p² + 5.p + 4
D'où la fonction de transfert :
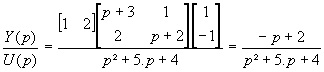
![]()
PLURALITE DES REPRESENTATIONS D'ETAT
Un vecteur d'état [ X ] évolue dans un espace de n dimensions et son extrémité décrit la trajectoire d'état. Dans un espace donné, tout vecteur d'état [ X ] est lié à un autre par une relation du type:
X = P.Z
P matrice de passage non singulière.Il existe donc une infinité de représentations pour un même système. Elles n'ont pas toutes un sens physique comme celles établies précédemment. Certaines représentations permettent cependant d'alléger considérablement les calculs ou de mettre en évidence des propriétés du système.
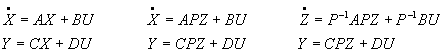
à identifier à :
|
|
Où l’indice i désigne la nature de la représentation d’état obtenue après changement de base. Les formes les plus communément rencontrées étant la forme diagonale d, la forme horizontale h et la forme verticale v. Dans les ouvrages spécialisés les formes compagnes horizontale et verticale sont parfois appelées respectivement forme compagne commandable et observable.
![]() Unicité de la fonction de transfert
Unicité de la fonction de transfert
La fonction de transfert est unique
quelle que soit la représentation d'état choisie. Le changement de base![]()
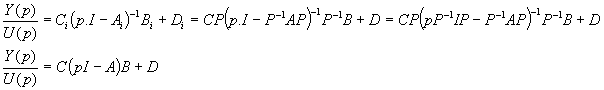
![]() LES FORMES CANONIQUES
LES FORMES CANONIQUES
L'objectif de la représentation d'état est d'aboutir pour les systèmes à l’élaboration d’une commande. A cet égard, certaines formes de représentation d'état se prêtent mieux que d'autres à l'interprétation des propriétés d'un système ou au bon déroulement des calculs.
Elle permet de mettre en évidence les modes du système, de conclure quant à sa stabilité ( existence éventuelle de pôles à partie réelle positive ) et sa dynamique ( notion de mode dominant, d’amortissement etc. ). Cette forme compagne est obtenue par diagonalisation de la matrice A. L'ordre de multiplicité des valeurs propres doit être égal à l'ordre de l'espace qu'engendrent les vecteurs propres. Si ce n'est pas le cas, une forme de Jordan s'impose ( cf §5.4 ).
![]() Rappels
Rappels
Soit A, une matrice d’évolution des états (n x n). Un scalaire l est appelé valeur propre de A s’il existe un vecteur d’état ![]() non nul pour lequel
non nul pour lequel ![]() . Avec li , les racines de PA(l)=det[l.I-A] le polynôme caractéristique de A.
. Avec li , les racines de PA(l)=det[l.I-A] le polynôme caractéristique de A.
Les vecteurs propres ![]() qui permettent de construire la matrice de passage P sont obtenus en résolvant
qui permettent de construire la matrice de passage P sont obtenus en résolvant ![]()
Après changement de base, on a :

avec :
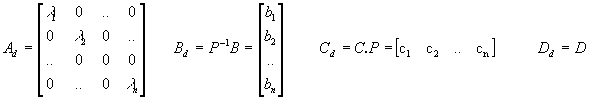
dont on déduit la représentation fonctionnelle :
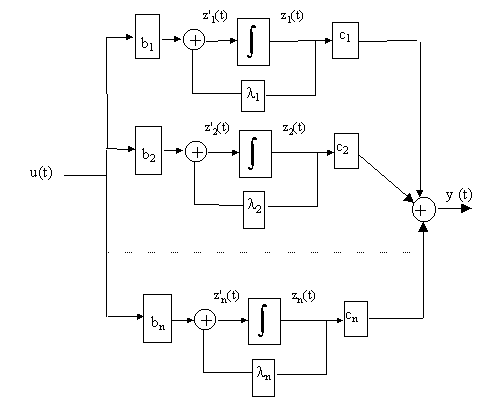
Figure 8
Comme le montre la figure 8, le système se ramène à la superpositition de n systèmes élémentaires du premier ordre, cette représentation fait apparaître immédiatement :
- la constante de temps propre à chaque variable d’état 1 / li,
- l’effet de la commande sur les états zi au travers de bi,
- la contribution des états à la réponse y au travers de ci.
![]() Exemple
Exemple
On reprend le système étudié au § 3.1.1.
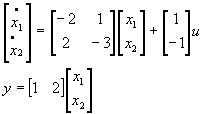
Calcul des valeurs propres
![]()
Deux valeurs propres distinctes -4 et -1 auxquelles sont associés deux vecteurs propres.
Calcul des vecteurs propres
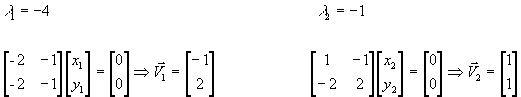
Soit
![]()
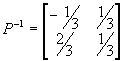
Les résultats établis au ( 3.1 ) permettent de donner la nouvelle représentation d'état :
Ad = P-1.A.P = ![]()
Bd= P-1.B = ![]()
Cd= C.P = [ 3, 3 ]
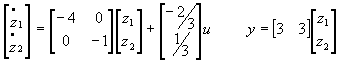
Interprétation
La mise sous forme de schéma fonctionnel fait clairement apparaitre les modes du système qui sont découplés.
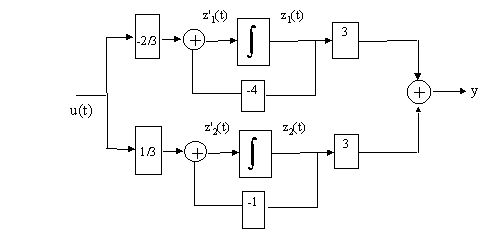
Figure 9
Dans cet exemple, on remarque que la commande permet d'agir sur chacun des états et que la sortie y(t) est une combinaison linéaire de tous ces états.
On passe aisément dans le domaine fréquentiel; en effet,

Les modes du système ne sont autres que les valeurs propres de la matrice A. On peut dès lors immédiatement conclure quant à la stabilité. Enfin on peut immédiatement passer à la fonction de transfert ( représentation externe ). On peut écrire :
Pour un système décrit par une représentation d'état, l'objectif est la commande de ce système, et ce dans le but d'améliorer ses performances ( stabilité, précision, rapidité, robustesse ...). Parmi les techniques de commande qui seront envisagées, on étudiera la commande par placement de modes. Une stratégie classique consiste par exemple à donner a un système les caractéristiques d'un second ordre avec temps de réponse minimal.
Le passage à la forme compagne horizontale facilite alors considérablement la mise en oeuvre d'une telle commande. L'écriture est la suivante :
|
|
Où les ai désignent les coefficients du polynôme caractéristique de la matrice d'évolution A : ![]()
La matrice de passage P vérifie :
Ah = P-1.A.P Û P.Ah = A.P Bh = P-1.B Û P.Bh = B
On pose : P = [ p1 p2 ...pn ]
On a alors : [ p1 p2 ...pn ].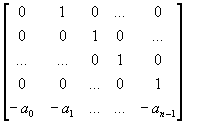 = A. [ p1 p2 ...pn ]
= A. [ p1 p2 ...pn ]
Il vient :
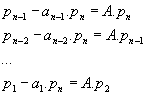
par ailleurs,
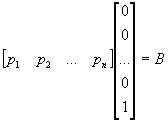 ð
ð
|
|
résultat qu'on réintroduit dans les équations des pi
|
" " " "
|
![]() Exemple
Exemple
Soit à mettre sous forme compagne horizontale le système défini par :
![]()
le polynôme caractéristique de A :
![]()
soit a0 = 4 et a1 = 5
la matrice de passage
p2 = B p1 = ( A + a1.I ).B
![]()
![]() ð
ð ![]()
dont on tire la représentation d’état sous forme compagne horizontale :
![]() La forme compagne verticale
La forme compagne verticale
Pour commander un processus par retour d'état, il faut pouvoir contrôler tous ses états. Cependant, pour des raisons pratiques ou économiques, il n'est pas toujours possible d'attribuer un capteur à chacun d'eux. On réalise donc des observateurs d'états qui ont pour fonction de reconstruire les états que l'on ne mesure pas ou qui sont impossibles à mesurer. La forme compagne verticale facilite notablement la mise en oeuvre des observateurs.
|
|
Où les ai désignent les coefficients du polynôme caractéristique de la matrice d'évolution A :
![]()
On se ramène au cas de la recherche de la matrice de passage pour une forme horizontale par transposition de Av et Cv.
La matrice de passage P vérifie alors :
Av = P-1.A.P ð (Av)T = PT.AT.(P-1)T ð (P-1)T.(Av)T = AT.(P-1)T
Cv = C.P ð (P-1)T.(Cv)T = CT
On pose comme précédemment (P-1)T = [ p1 p2 ...pn ]
Il vient : pn = CT
![]()
" " " " " " " "
![]()
Il faut ensuite inverser et transposer P pour trouver la matrice de passage souhaitée.
![]() Exemple
Exemple
![]()
p2 = CT = ![]() p1 = ( AT + a1.I ).CT =
p1 = ( AT + a1.I ).CT = ![]()
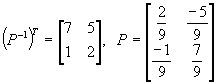
Il en résulte la représentation :
![]()
Dans le cas où le système possède des pôles multiples, la fonction de transfert s'écrit :
![]()
elle peut-être représentée par :

Figure 11
Cette représentation fait apparaître de façon évidente les variables d'état dont on sait qu'elles représentent des facteurs d'énergie. Elles sont naturellement présentes en sortie des intégrateurs ( termes en 1 / p ). La figure 11 fait apparaitre immédiatement une représentation d'état.
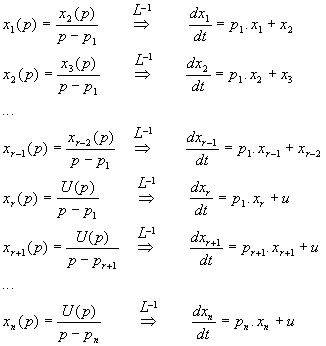
Soit sous forme matricielle :

![]()
![]() OBTENTION DE LA REPRESENTATION D'ETAT DEPUIS LA FONCTION DE TRANSFERT
OBTENTION DE LA REPRESENTATION D'ETAT DEPUIS LA FONCTION DE TRANSFERT
On cherche à obtenir une représentation d’état d’un système possédant une seule entrée et une seule sortie à partir de la fonction de transfert . Il faut cependant prendre garde au fait qu'une fonction de transfert ne décrit pas avec autant de précision un processus qu'une représentation d'état. Ces résultats seront mis en évidence au chapitre II. On fait ici l’hypothèse que la fonction de transfert porte toutes les informations contenues das la représentation d’état.
Soit : ![]()
et n ³ m
On l’obtient après décomposition en éléments simples de la fonction de transfert. Selon que les valeurs propres sont d’ordre multiple ou non, on se ramène à une forme de Jordan ou à une forme diagonale ( Cf § 5.1.3 et 5.4 ).
![]() Obtention d’une forme compagne horizontale
Obtention d’une forme compagne horizontale
On cherche dans un premier temps à obtenir une forme compagne horizontale. On divise numérateur et dénominateur par pn.
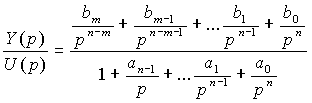
puis on introduit une fonction V(p) telle que :
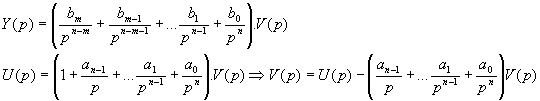
équations dont on extrait un schéma fonctionnel,
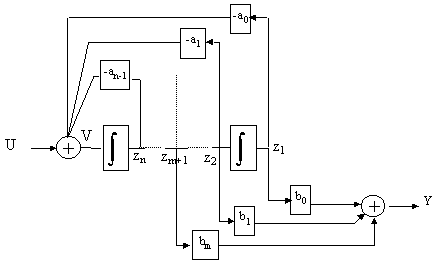
Figure 12
Avec les variables d’état choisies, on aboutit à une forme compagne horizontale :
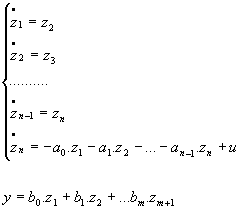
![]() Obtention d’une forme compagne verticale
Obtention d’une forme compagne verticale
On passe de la fonction de transfert à la forme compagne verticale en extrayant l’observation Y(p).
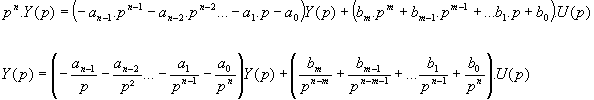
dont on tire le schéma :

Figure 13

Sous forme matricielle :

![]()
![]() INTEGRATION DE L'EQUATION D'ETAT
INTEGRATION DE L'EQUATION D'ETAT
Considérons un processus continu d'équation d'état : 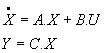
Evoluant sous l'effet d'une entrée u(t) à partir de la condition initiale X(t0) = X0 . L'intégration de cette équation par la méthode de variation de la constante ( démontrée en annexe 1 ) conduit pour x à :
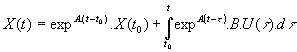
et la sortie :
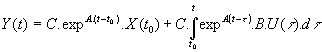
La réponse est la somme d'un régime libre ( qui dépend de l'état initial ) et d'un régime forcé (qui dépend de la commande ). La résolution de ce problème est aisée lorsque le système peut être mis sous forme diagonale puisqu’il se ramène résoudre n équations différentielles du premier ordre indépendantes entre elles. Plus généralement, la résolution de l'équation d'état nécessite le calcul de l’exponentielle de matrice : expAt encore appelée matrice de transition.
L’expression de expAt est obtenu en utilisant la formule de Sylvester démontrée en annexe 2.
![]()
avec ![]() où li est la i-ème valeur propre de A.
où li est la i-ème valeur propre de A.
Cette méthode nécessite la connaissance des valeurs propres de A qui doivent être distinctes.
Exemple
![]()
Les valeurs propres de A calculées au 4.1 sont –4 et –1.
![]() ð
ð 
On obtient alors :
![]() ð
ð 
La transformée de Laplace ( notée L ) appliquée à l'équation d'état matricielle :
![]() ð
ð ![]()
Cette dernière équation a pour solution
![]()
Par analogie avec la transformée de Laplace ( notée L ) de ![]() , on en déduit le résultat très important :
, on en déduit le résultat très important :
|
|
La matrice qu'on inverse doit être régulière. Cette méthode qui nécessite le calcul de l'inverse d'une matrice et le retour à l'original, convient tant que l'ordre de A est peu élevé.
Exemple
(p.I - A)-1 = 
On décompose en éléments simples,
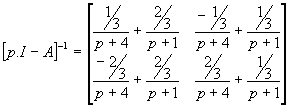
Retour à l'original,

![]() Propriétés de la matrice de transition
Propriétés de la matrice de transition
La matrice de transition notée f(t) possède les propriétés suivantes démontrées en annexe 1 :
ð
ð
ð
De la dernière relation, il découle :
ð
![]() Résolution de l'équation d'état
Résolution de l'équation d'état
Traitons la au travers de l'exemple précédent. On a établi : 
![]() Régime libre
Régime libre
On calcule dans un premier temps le régime libre, les conditions initiales choisies étant ![]() , la commande est un échelon unitaire. On prend t0 = 0.
, la commande est un échelon unitaire. On prend t0 = 0.
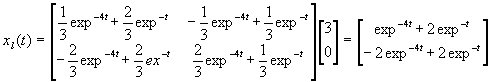
![]() Régime forcé
Régime forcé
![]()

![]()

Enfin ![]()
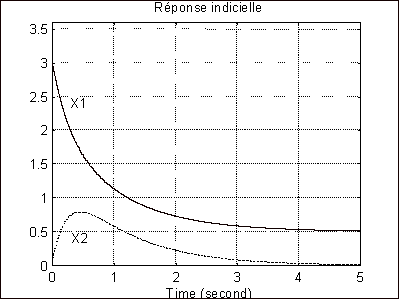
Figure 15
![]()