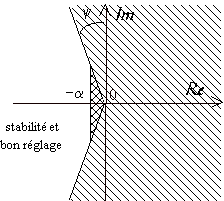
4-3 Degré de stabilité dans le plan d'Evans
On a vu qu'un système pouvait être stable, mais posséder des modes convergeant trop lentement vers leur valeur de repos (pôles trop près de l'axe imaginaire).
On définit donc dans le plan d'Evans une marge de
stabilité absolue, qui consiste à régler le gain de telle
sorte que tous les pôles du système se trouvent à gauche de la
droite d'équation ![]() ,
avec
,
avec ![]() (on impose
en fait que tous les modes décroissent plus rapidement que
(on impose
en fait que tous les modes décroissent plus rapidement que ![]() ).
).
De la même manière, un système stable pouvant posséder des modes oscillatoires mal amortis, on définit aussi dans le plan d'Evans une marge de stabilité relative, qui consiste à imposer à tous les modes complexes qu'ils aient un amortissement réduit x supérieur à arcsin y .
Ces deux marges de stabilité se traduisent graphiquement de la manière suivante: