2-3 Critère du revers

a - Dans le plan de Nyquist

Lorsque la FTBO du système ne possède aucun pôle à partie réelle positive, et compte tenu de la symétrie du contour parcouru, on peut simplifier le critère de Nyquist de la manière suivante:

Un système stable en boucle ouverte est stable en boucle fermée si et seulement si le lieu de Nyquist de sa FTBO, parcouru dans le sens des w croissants, laisse à gauche le point critique.

Ce critère simplifié est appelé critère du revers.

b - Dans le plan de Black

Dans le plan de Black, le critère du revers s'énonce de la façon suivante:

Un système stable en boucle ouverte est stable en boucle fermée si et seulement si le lieu de Black-Nichols de sa FTBO, parcouru dans le sens des w croissants, laisse à droite le point critique.

c - Synthèse du critère du revers

Le tableau suivant regroupe quelques exemples illustrant l'énoncé du critère du revers dans les plans de Black et de Nyquist:

	dans le plan de Black
système stable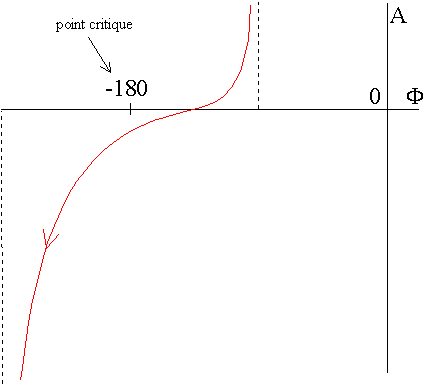
système instable