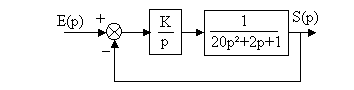
2-1 Critère algébrique de Routh-Hurwitz

Le calcul des racines de l'équation caractéristique du système n'est pas toujours aisé, en particulier si l'ordre du système est important ou si ce système comprend des paramètres que l'on veut régler.

Exemple: Réglage d'un gain.

Le critère de Routh-Hurwitz permet de déterminer si un système est stable ou non, sans qu'il soit nécessaire de calculer les racines de l'équation caractéristique.

a - Enoncé du critère

Soit un système linéaire de fonction de transfert H(p).

Le dénominateur de H(p) peut être mis sous la forme , avec an > 0.

On peut démontrer aisément que le système est instable si l'un au moins des coefficients ai est négatif ou nul (car, dans ce cas, D(p) admet au moins une racine à partie réelle positive ou nulle).

Une condition nécessaire est donc que tous les coefficients ai soient strictement positifs.

Cette condition n'étant pas suffisante, on construit alors le tableau de Routh de la manière suivante:

- chaque ligne comprend les coefficients d'un polynôme d'ordre décroissant (de n à 0),

- les deux premières lignes sont écrites à partir du dénominateur de la fonction de transfert,

- les autres lignes sont calculées comme indiqué.

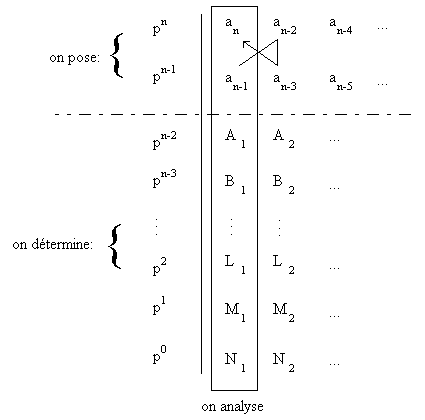
- Calculs -

La présence d'un zéro à la fin de chaque ligne entraîne le raccourcissement de la ligne suivante. Les deux dernières lignes ne comportent plus qu'un seul coefficient différent de zéro.

Le critère de Routh-Hurwitz s'exprime de la façon suivante:

Un système d'équation caractéristique (avec an>0) est stable si et seulement si:

- ,

- tous les termes de la première colonne du tableau de Routh sont positifs.

Remarque: Si tel n'est pas le cas, le nombre de racines de D(p) à partie réelle positive ou nulle est égal au nombre de changements de signes dans cette colonne.

b - Cas particuliers et remarque

Premier cas particulier: un zéro apparaît dans la première colonne.

Dans ce cas, il n'est plus possible de construire les lignes suivantes du tableau de Routh. Deux méthodes sont alors possibles:

- soit on forme le polynôme et on construit son tableau de Routh.

- soit on remplace le zéro par un e et on analyse l'évolution des termes suivants du tableau lorsque e tend vers zéro par valeurs positives.

Deuxième cas particulier: tous les termes d'une ligne sont nuls.

L'équation caractéristique admet deux racines imaginaires purs conjuguées . On procède alors de la manière suivante:

- à partir des coefficients de la dernière ligne non nulle, on construit le polynôme auxiliaire Paux (p), dont les racines sont ,

- on calcule ,

- on remplace la ligne nulle par les coefficients de ce polynôme dérivé,

- on poursuit la construction du tableau de Routh.

Remarque:

Le critère de Routh-Hurwitz possède un avantage indéniable: il ne nécessite pas la factorisation de D(p).

En revanche, il n'explicite pas les modes du système (i.e. les racines du dénominateur de la fonction de transfert). Enfin, il ne s'applique qu'aux transmittances rationnelles.

c - Exemples

Exemple 1

Reprenons l'exemple précédent:

Construisons le tableau de Routh correspondant:

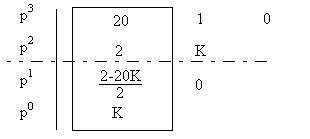
Les deux conditions de stabilité sont donc:

soit

Exemple 2

Soit

Construisons le tableau de Routh correspondant:

Un zéro apparaît dans la première colonne.

On ne peut poursuivre la construction du tableau de Routh.

On utilise alors l'une des deux méthodes décrites précédemment:

Exemple 3

Soit enfin

Construisons le tableau de Routh correspondant:

On se trouve dans le cas particulier où une ligne complète est nulle.

On pose donc

d'où

Il reste à remplacer la ligne nulle par les coefficients de ,

ce qui donne:

Tous les coefficients de la première colonne sont positifs, l'équation caractéristique du système ne possède donc que des racines à partie réelle négative, en plus des deux racines imaginaires purs conjugués.

Le système n'est donc pas stable, il possède un mode oscillant non amorti.