1-2 Condition de stabilité
Considérons un système linéaire continu, initialement au repos, de fonction de transfert H(p).
Un tel système est stable si, soumis à une perturbation, il tend à revenir à sa position de repos. Autrement dit, sa réponse impulsionnelle doit tendre vers zéro lorsque t tend vers l'infini.
Or, on sait que la fonction de transfert d'un système est la
transformée de Laplace de sa réponse impulsionnelle (![]() car E(p) = 1).
car E(p) = 1).
La décomposition en éléments simples de H(p), qui permet le calcul de l'original de H(p), donne donc directement s(t).
En supposant qu'il n'y a pas de pôles multiples, cette décomposition en éléments simples s'exprime de la façon suivante:
![]()
où les pi sont les pôles, réels ou complexes conjugués, de la fonction de transfert. Soit encore, en séparant les pôles réels des pôles complexes, et en regroupant les pôles complexes conjugués:
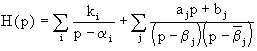
Et par conséquent:
![]()
Il suffit donc que l'une des exponentielles ne tende pas vers zéro (lorsque t tend vers l'infini) pour que le système ne revienne pas à sa position de repos.
C'est le cas lorsque l'une au moins des exponentielles possède un exposant positif ou nul, comme le montrent les tableaux suivants:
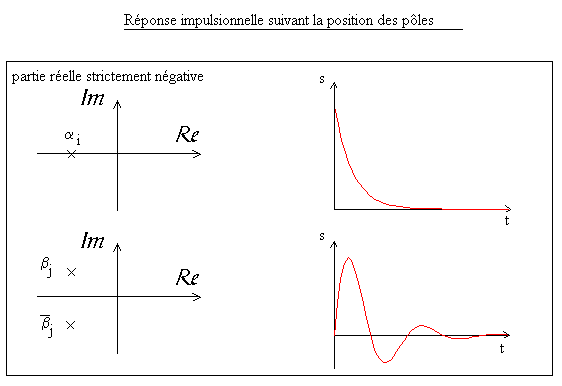
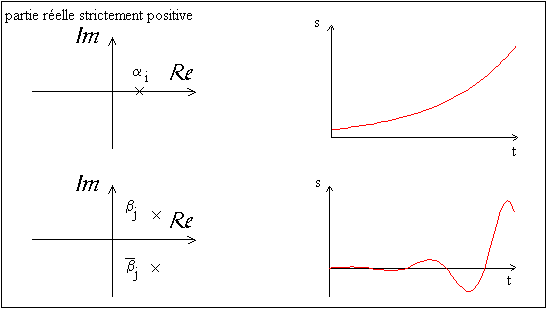
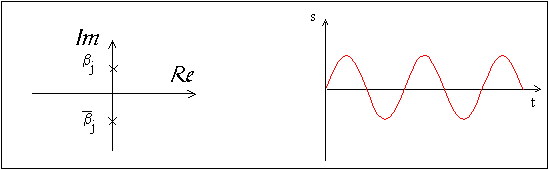
Une condition nécessaire et suffisante de stabilité d'un système est donc que tous les pôles de sa fonction de transfert soient à partie réelle strictement négative.