3-2 Notion de modes dominants
Le résultat de l'étude d'un système par découpage en sous-systèmes simples peut très rapidement devenir compliqué.
Néanmoins, l'analyse de la place des différents pôles dans le plan complexe peut donner une idée assez précise du comportement du système complet, et notamment faire apparaître d'éventuels modes dominants.
Les modes dominants correspondent aux pôles qui influencent le plus la réponse du système complet. A gains statiques partiels équivalents, ces pôles sont ceux qui se situent le plus près de l'axe imaginaire, c'est à dire ceux dont les constantes de temps associées sont les plus élevées (pour les sous-systèmes du 1er ordre) ou ceux dont les amortissements réduits associés sont les plus faibles (pour les sous-systèmes du 2ème ordre).
Exemple 1: Soit le système de transmittance: ![]()
La décomposition en éléments simples de H(p) donne:
![]()
On a donc:
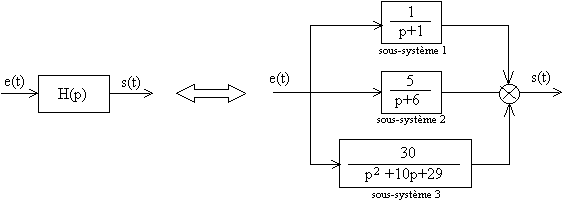
La place des différents pôles dans le plan complexe est donc la suivante:
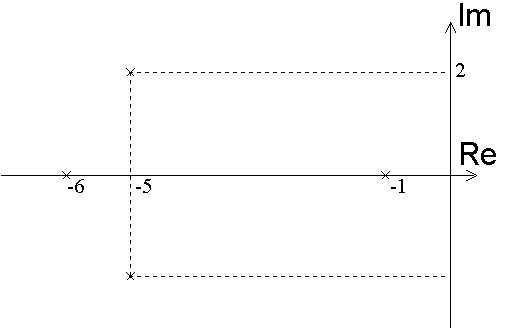
Les gains statiques partiels des différents sous-systèmes étant du même ordre de grandeur, l'analyse de la place des pôles dans le plan complexe nous permet de dire que le système complet aura un comportement proche de celui du sous-système 1. Le sous-système 1 correspond au mode dominant du système.
L'allure de la réponse indicielle du système complet nous confirme ce résultat:
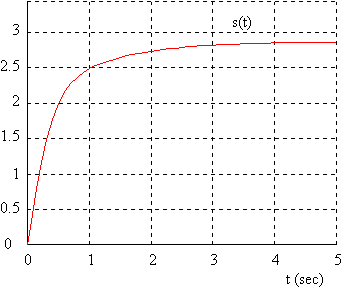
Exemple 2: Soit le système de transmittance: ![]()
La décomposition en éléments simples de H(p) donne:
![]()
On a donc:
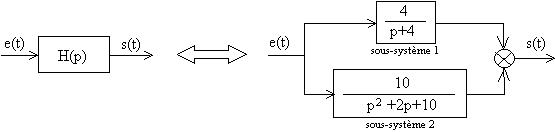
La place des différents pôles dans le plan complexe est donc la suivante:
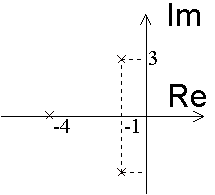
Les gains statiques partiels des deux sous-systèmes étant égaux, l'analyse de la place des pôles dans le plan complexe nous permet de dire que le système complet aura un comportement proche de celui du sous-système 2. Le sous-système 2 correspond au mode dominant du système.
L'allure de la réponse indicielle du système complet nous confirme ce résultat:
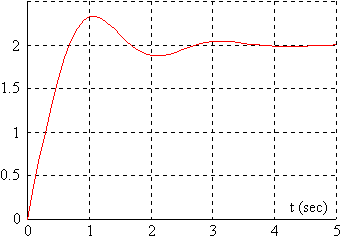
Remarque: lorsque les gains statiques partiels ne sont pas équivalents, une analyse plus fine doit être menée.