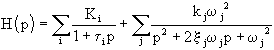
3-1 Généralités
Considérons un système du nième ordre (n>2), de fonction de transfert H(p).
Ce système admet donc n pôles, que l'on supposera distincts. Ces pôles sont réels ou complexes conjugués.
Si l'on décompose H(p) en une somme d'éléments simples, on obtient donc:
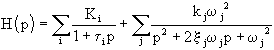
Les termes du 1er ordre correspondent aux pôles réels, ceux du 2ème ordre aux pôles complexes conjugués regroupés par paire.
Le système complet apparaît donc comme la somme de plusieurs sous-systèmes simples:
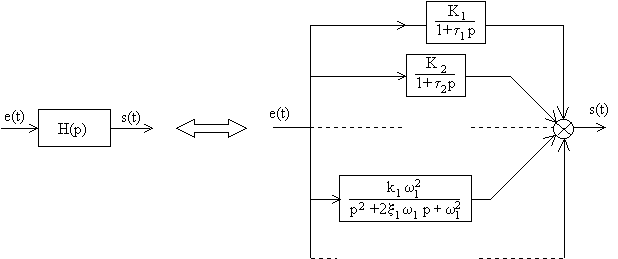
La réponse du système complet à une entrée donnée est donc la superposition des réponses des différents sous-systèmes à cette même entrée.
Une entrée quelconque pouvant être décomposée en une combinaison d'entrées-type, et la réponse des systèmes simples aux entrées-type étant connue, la réponse du système complet peut être déterminée.
Notons que, si l'un des sous-systèmes est instable, le système complet est instable.