), on a 
et 
.2-4 Construction du diagramme de Bode et des lieux de transfert
a - Diagramme de Bode
Aux basses fréquences (), on a et .
La courbe de gain possède une asymptote (horizontale) quand w ® 0.
La courbe de phase part de 0°
Aux hautes fréquences (
), on a 
et 
.
La courbe de gain possède une asymptote (oblique) quand w ® ¥ , d'équation
et de pente -40 dB/décade, soit -12 dB/octave (on dit aussi parfois "de pente -2").
Les deux asymptotes de la courbe de gain se rencontrent au
point d'abscisse 
.
Ce point est aussi un point d'inflexion dans la courbe de phase.
En ce point, la phase vaut exactement -90°.
La courbe de phase vient tangenter -180°
Aux fréquences moyennes (
), l'allure des courbes dépend
essentiellement de la valeur de x .
Sur la courbe de phase, on observe une variation de phase
autour du point 
d'autant
plus rapide que x est petit.
Pour x < 0,7 (
exactement), on
observe que la courbe de gain passe par un maximum, d'autant plus
grand que x est petit.
Ce maximum, appelé facteur de surtension du système,
vaut: 
.
Il est obtenu pour une pulsation dite pulsation de
résonance 
.
Le tableau suivant donne la valeur de Q et celle du dépassement à la résonance pour quelques valeurs particulières de x :
| x | 0,4 |
0,425 |
0,5 |
0,6 |
0,7 |
> 0,7 |
| Q (dB) | 2,7 |
2,3 |
1,25 |
0,35 |
0 |
- |
| D1% | 36% |
30% |
16% |
4% |
0% |
- |
La courbe ci-dessous donne l'évolution de Q en fonction de x :
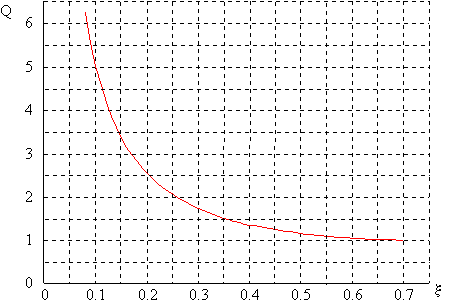
Les diagrammes de Bode ont donc l'allure suivante:
courbe de gain:
courbe de phase:
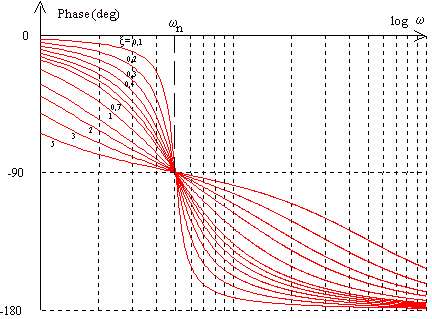
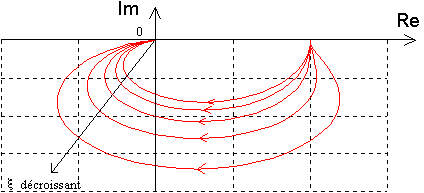
b - Lieu de Nyquist
Le lieu de Nyquist d'un système du 2ème ordre a l'allure suivante:
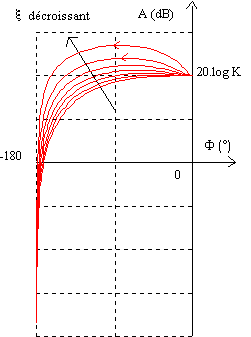
c - Lieu de Black-Nichols
Le lieu de Black-Nichols se déduit du diagramme de Bode. Il a l'allure suivante:
