1-4 Construction du diagramme de Bode et des lieux de transfert
a - Diagramme de Bode
On a:
Aux basses fréquences (
), on a 
et 
.
La courbe de gain possède une asymptote (horizontale) quand w ® 0.
Aux hautes fréquences (
), on a 
et 
.
La courbe de gain possède une asymptote (oblique) quand w ® ¥ , d'équation 
. C'est donc une droite de pente -20
dB/décade, soit -6 dB/octave (on dit aussi parfois "de
pente -1").
Les deux asymptotes de la courbe de gain se rencontrent au
point d'abscisse 
:
c'est la pulsation de coupure du système. Ce point est
aussi un point d'inflexion dans la courbe de phase.
La courbe de gain réelle se trouve 3 dB en dessous de ce point (c'est pourquoi on parle aussi de pulsation de coupure à -3dB).
Le tableau ci-dessous récapitule, pour quelques valeurs particulières de w , la position de la courbe de gain réelle par rapport aux asymptotes et la valeur de la phase correspondante:
| pulsation |
|
|
|
| position ÷ asymptotes | -1 dB |
-3 dB |
-1 dB |
| phase F | -26,5° |
-45° |
-63,5° |
courbe de gain:
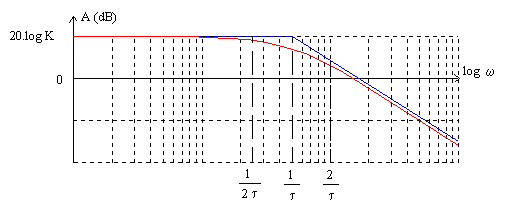
courbe de phase:
b - Lieu de Nyquist
.
d'où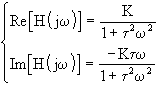 
On vérifie que: 
Le lieu de Nyquist d'un système du 1er ordre est un demi-cercle de diamètre K:
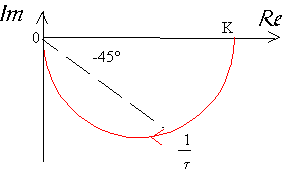
c - Lieu de Black-Nichols
On a: 
donc 
, 
soit 
L'utilisation du diagramme de Bode pour le tracé du lieu de Black-Nichols facilite le paramétrage en w de la courbe.
Le lieu de Black-Nichols d'un système du 1er ordre a donc l'allure suivante:
